Question

17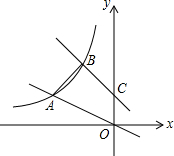．直线y=-x+1交y轴于C点，直线y=-$\frac{1}{2}$x，两条直线分别交双曲线y=$\frac{k}{x}$（x＜0）于B、A两点，若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$．
（1）求k的值；
（2）求四边形OABC的面积．

Answer 1

分析 （1）设点A的坐标为（m，-$\frac{1}{2}$m），点B的坐标为（n，-n+1），由此得出OA及BC的长度，结合OA、BC间的比例可得出m=2n，再结合反比例函数图象上点坐标的特征可求出m、n、k的值．
（2）过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，作BE⊥y轴于点F，通过分割五边形ADOFB，结合三角形、梯形的面积公式即可求出四边形OABC的面积．

解答 解：（1）设点A的坐标为（m，-$\frac{1}{2}$m），点B的坐标为（n，-n+1），
则OA=-$\frac{\sqrt{5}}{2}$m，BC=-$\sqrt{2}$n，
∵$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$，
∴m=2n．
又∵k=m•（-$\frac{1}{2}$m）=n•（-n+1），
解得：$\left\{\begin{array}{l}{n=-1}\\{k=-2}\end{array}\right.$或$\left\{\begin{array}{l}{n=0}\\{k=0}\end{array}\right.$（舍去）．
故k的值为-2．
（2）过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，作BE⊥y轴于点F，如图所示．

∵n=-1，m=2n=-2，
∴点A的坐标为（-2，1），点B的坐标为（-1，2），
令y=-x+1中的x=0，则y=1，
∴点C的坐标为（0，1）．
∴S_{四边形AOCB}=S_矩形BEOF+S_梯形ADEB-S_△AOD-S_△BCF，
=|k|+$\frac{1}{2}$（AD+BE）•DE-$\frac{1}{2}$|k|-$\frac{1}{2}$BF•CF，
=2+$\frac{1}{2}$×（1+2）×1-$\frac{1}{2}$×2-$\frac{1}{2}$×1×1，
=2+$\frac{3}{2}$-1-$\frac{1}{2}$，
=2．

点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征、反比例函数系数k的几何意义、三角形的面积公式以及梯形的面积公式，解题的关键是：（1）依照比例找出m=2n；（2）分割图形求面积．本题属于基础题，难度不大，解决该题型题目时，通过分割图形再结合反比例函数系数k的几何意义得出所求图形的面积是关键．