题目内容
6．设a，b是方程x2+x-2009=0的两个实数根，求a2+2a+b的值．分析 由于a2+2a+b=（a2+a）+（a+b），故根据方程的解的意义，求得（a2+a）的值，由根与系数的关系得到（a+b）的值，即可求解．
解答 解：∵a，b是方程x2+x-2009=0的两个实数根，
∴a2+a-2009=0，即a2+a=2009，a+b=-1，
∴a2+2a+b=a2+a+a+b=2009-1=2008．
点评 本题综合考查了一元二次方程的解的定义及根与系数的关系，要正确解答本题还要能对代数式进行恒等变形．
练习册系列答案
相关题目
计算：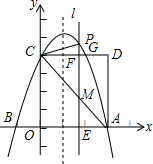
如图，二次函数y=ax2-2ax+4（a≠0）的图象交x轴于点A、B，点A坐标为（3，0），与y轴交于点C，以OC、OA为边作矩形OADC，点E位线段OA上的动点，过点E作x轴的垂线分别交CA、CD和二次函数的图象于点M、F、P，连接PC．
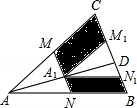如图，如图，M、N分别是△ABC的边AC和AB的中点，D为BC上任意一点，连接AD，将△AMN沿AD方向平移到△A1M1N1的位置，且M1N1在BC边上，已知△AMN的面积为7，则图中阴影部分的面积为14．
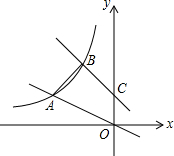直线y=-x+1交y轴于C点，直线y=-$\frac{1}{2}$x，两条直线分别交双曲线y=$\frac{k}{x}$（x＜0）于B、A两点，若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$．