题目内容
6.如果一次函数y=2x+m-1的图象不经过第二象限,则m的取值范围是m≤1.分析 根据函数的解析式可知,一次函数的斜率大于0,则函数必过一、三象限;如果函数图象不过第二象限,则函数必交y轴于负半轴(或原点),即m-1≤0,由此可求得m的取值范围.
解答 解:∵一次函数y=2x+m-1的图象不经过第二象限,
∴m-1≤0,
解得 m≤1.
故答案是:m≤1.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时,函数的图象经过一、三、四象限是解答此题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
14.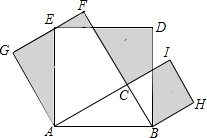 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )| A. | 60 | B. | 90 | C. | 144 | D. | 169 |
18.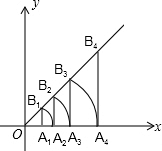 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
 如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )
如图,平面坐标系内,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…按此作法进行去,点Bn(n为正整数)的横坐标为( )| A. | ($\sqrt{2}$)n-1 | B. | ($\sqrt{2}$)n | C. | ($\sqrt{2}$)n+1 | D. | 2n |
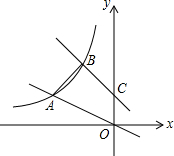 直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.
直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.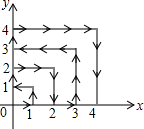 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).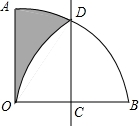 如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)
如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)