题目内容
2. Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.
Rt△ABC中,∠B=90°,∠BAC=78°,过C作CF∥AB,连接AF与BC相交于G,若GF=2AC,求∠BAG的大小.
分析 采用折半法,把GF一分为二,构造直角三角形斜边上的中线,可得到3个等腰三角形,设出∠F=x°,通过角的计算即可得出关于x的一元一方程,解方程即可得出结论.
解答 解:取FG的中点D,连接CD,如图所示.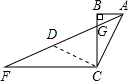
设∠F=x°,
∵∠B=90°,CF∥AB,
∴∠BAG=x°,∠BCF=90°,
∴DC=DF=DG.
又∵GF=2AC,
∴AC=DC=DF=DG,
∴∠ADC=∠DAC=2x°.
∵∠BAC=78°,
∴3x°=78°,
∴∠BAG=∠F=x°=26°.
点评 本题考查了平行线的性质以及角的计算,解题的关键是构造三个等腰三角形.本题属于基础题,难度不大,在解决该题型题目时,根据已知的边角关系想办法尽可能多的找出相等的角,该题中巧妙的选用了FG的中点D,通过三个等腰三角形找出所要求的角与已知角间的关系,从而得以解决.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
10.已知Rt△ABC中,∠C=90°,∠A的正弦是( )
| A. | $\frac{BC}{AB}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BC}{AC}$ | D. | $\frac{AB}{BC}$ |
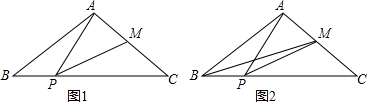 如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.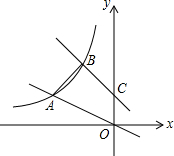 直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.
直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.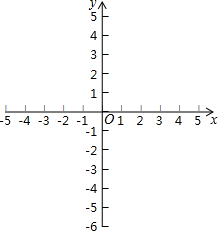 已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.
已知直线l:y=-2x+2,且点T(t,$\frac{2}{3}$)在直线l上.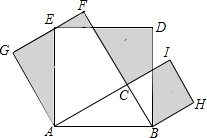 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,则图中阴影部分的面积之和( )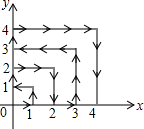 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).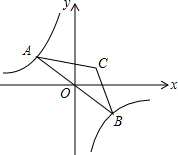 如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.