题目内容
13. 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )| A. | $\frac{25}{2}$cm2 | B. | 10cm2 | C. | 5$\sqrt{6}$cm2 | D. | 以上都有可能 |
分析 因为等腰三角形腰的位置不明确,所以分(1)腰长在矩形相邻的两边上,(2)一腰在矩形的宽上,(3)一腰在矩形的长上,三种情况讨论.(1)△AEF为等腰直角三角形,直接利用面积公式求解即可;(2)先利用勾股定理求出AE边上的高BF,再代入面积公式求解即可;(3)先求出AE边上的高DF,再代入面积公式求解即可.
解答 解:分三种情况计算:
(1)当AE=AF=5厘米时,
∴S△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×5×5=12.5厘米2,
(2)当AE=EF=5厘米时,如图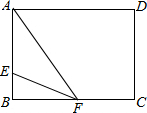
BF=$\sqrt{E{F}^{2}-B{E}^{\;}}$=2$\sqrt{6}$厘米,
∴S△AEF=$\frac{1}{2}$•AE•BF=$\frac{1}{2}$×5×2$\sqrt{(\;\;\;\;)}$=5$\sqrt{6}$厘米2,
(3)当AE=EF=5厘米时,如图
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=4厘米,
∴S△AEF=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×5×4=10厘米2,
故选D.
点评 本题主要考查矩形的角是直角的性质和勾股定理的运用,要根据三角形的腰长的不确定分情况讨论是解题的关键也是此题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.sin30°=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.抛物线y=x2+2x+2-m与x轴有两个交点,则下列m的值符合题意的是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
5.盐阜商场试销一种品牌服装,成本为每件300元,规定试销期间销售单价不低于成本单价,且获利不得高于20%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 330 | 335 | 340 | 345 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
 如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.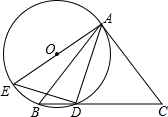 如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE.
如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE. 如图,过正五边形ABCDE的顶点A作直线AF∥CD,则∠EAF的度数为36°.
如图,过正五边形ABCDE的顶点A作直线AF∥CD,则∠EAF的度数为36°.