Question

2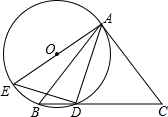．如图，△ABC中，AB=AC，点D为BC边上一点，且DA=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连接DE．
（1）求证：AC是⊙O的切线；
（2）若sinC=$\frac{4}{5}$，AC=12，求⊙O的直径．

Answer 1

分析 （1）根据等腰三角形的性质，由AB=AC，AD=DC得∠C=∠B，∠1=∠C，则∠1=∠B，根据圆周角定理得∠E=∠B，∠ADE=90°，所以∠1+∠EAD=90°，然后根据切线的判定定理即可得到AC是⊙O的切线；
（2）过点D作DF⊥AC于点F，如图，根据等腰三角形的性质得CF=$\frac{1}{2}$AC=3，在Rt△CDF中，利用正弦定义得sinC=$\frac{DF}{DC}$=$\frac{4}{5}$，则设DF=4x，DC=5x，利用勾股定理得CF=3x，所以3x=3，解得x=1，于是得到DC=AD=5，然后证明△ADE∽△DFC，再利用相似比可计算AE即可．

解答 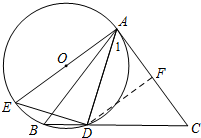（1）证明：∵AB=AC，AD=DC，
∴∠C=∠B，∠1=∠C，
∴∠1=∠B，
又∵∠E=∠B，
∴∠1=∠E，
∵AE是⊙O的直径，
∴∠ADE=90°，
∴∠E+∠EAD=90°，
∴∠1+∠EAD=90°，即∠EAC=90°，
∴AE⊥AC，
∴AC是⊙O的切线；

（2）解：过点D作DF⊥AC于点F，如图，
∵DA=DC，
∴CF=$\frac{1}{2}$AC=6，
在Rt△CDF中，∵sinC=$\frac{DF}{DC}$=$\frac{4}{5}$，
设DF=4x，DC=5x，
∴CF=$\sqrt{C{D}^{2}-D{F}^{2}}$=3x，
∴3x=6，解得x=2，
∴DC=10，
∴AD=10，
∵∠ADE=∠DFC=90°，∠E=∠C，
∴△ADE∽△DFC，
∴$\frac{AE}{DC}$=$\frac{AD}{DF}$，即$\frac{AE}{10}=\frac{10}{8}$=$\frac{5}{4}$，解得AE=$\frac{25}{2}$，
即⊙O的直径为$\frac{25}{2}$．

点评 本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了等腰三角形的性质和相似三角形的判定与性质．