题目内容
15. 如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
分析 (1)首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;
(2)连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.
解答 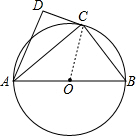 (1)解:∵AB是⊙O直径,C在⊙O上,
(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4;
(2)证明:连接OC
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.
点评 此题主要考查的是切线的判定方法.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
6.在一个不透明的口袋中装有6个红球,2个绿球,这些球除颜色外无其他差别,从这个袋子中随机摸出一个球,摸到红球的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
20.不等式组$\left\{\begin{array}{l}{x+5>0}\\{2x<6}\end{array}\right.$解集是( )
| A. | x>-5 | B. | x<3 | C. | -5<x<3 | D. | x<5 |
7.下列运算正确的是( )
| A. | a2+a2=a4 | B. | a5-a3=a2 | C. | a2•a2=2a2 | D. | (a5)2=a10 |
13. 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )| A. | $\frac{25}{2}$cm2 | B. | 10cm2 | C. | 5$\sqrt{6}$cm2 | D. | 以上都有可能 |
 如图,直线AB与坐标轴分别交于A(-2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.
如图,直线AB与坐标轴分别交于A(-2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式. 如图所示,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔4海里的A处,该海轮沿南偏东30°方向航行4海里后,到达位于灯塔P的正东方向的B处.
如图所示,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔4海里的A处,该海轮沿南偏东30°方向航行4海里后,到达位于灯塔P的正东方向的B处.