题目内容
18.抛物线y=x2+2x+2-m与x轴有两个交点,则下列m的值符合题意的是( )| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
分析 抛物线与x轴有两个交点,则△=b2-4ac>0,从而求出m的取值范围.
解答 解:∵抛物线y=x2+2x+2-m与x轴有两个交点,
∴△=b2-4ac>0,
即22-4×1×(2-m)>0,
解得:m>1,
所以D符合题意,故选D.
点评 本题考查了二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,注意:△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点是解答此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.不等式组$\left\{\begin{array}{l}{x+5>0}\\{2x<6}\end{array}\right.$解集是( )
| A. | x>-5 | B. | x<3 | C. | -5<x<3 | D. | x<5 |
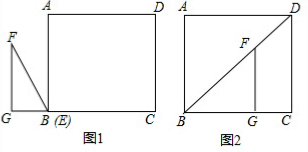
13. 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
 如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为( )| A. | $\frac{25}{2}$cm2 | B. | 10cm2 | C. | 5$\sqrt{6}$cm2 | D. | 以上都有可能 |
 已知:线段c,直线l及l外一点A.
已知:线段c,直线l及l外一点A.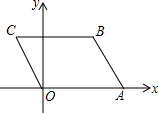 如图,已知A(4,0),B(3,3),以OA、AB为边作?OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为y=-$\frac{3}{x}$.
如图,已知A(4,0),B(3,3),以OA、AB为边作?OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为y=-$\frac{3}{x}$.