题目内容
17.已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.

分析 (1)根据等腰三角形两底角相等∠B=∠C,再根据平行线的性质得出,∠AFE=∠B,∠AEF=∠C,得出∠AFE=∠AEF,进一步得出结论;
(2)求出AE=AF,再根据旋转的性质可得∠E′AC=∠F′AB,AE′=AF′,然后利用“边角边”证明△CAE′和△BAF′全等,根据全等三角形对应边相等证明即可;
(3)把△AEF绕点A逆时针旋转AE′与过点C与AB平行的直线相交于M、N,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠C,
∵EF∥BC,
∴∠AFE=∠B,∠AEF=∠C,
∴∠AFE=∠AEF,
∴AE=AF.
(2)解:①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,
在△CAE′和△BAF′中,
$\left\{\begin{array}{l}{AE′=AF′}\\{∠E′AC=∠F′AB}\\{AB=AC}\end{array}\right.$,
∴△CAE′≌△BAF′(SAS),
∴CE′=BF′=6;
②由(1)可知AE=BC,
所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,
①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,
所以,∠BAM=∠ABC=72°,
又∵∠BAC=36°,
∴α=∠CAM=36°;
②当点E的像E′与点N重合时,
∵CE′∥AB,
∴∠AMN=∠BAM=72°,
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180°-72°×2=36°,
∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,
综上所述,当旋转角α为36°或72°.
点评 此题主要考查了旋转的性质以及等腰三角形的性质和等腰梯形的性质等知识,根据数形结合熟练掌握相关定理是解题关键.

①有两边和一角对应相等的两个三角形全等;
②有一个角为100°,且腰长对应相等的两个等腰三角形全等;
③有两边及第三边上的高对应相等的两个三角形全等;
④三条边对应相等的两个三角形对应角也是相等的.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③-$\sqrt{17}$是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
| A. | 2 | B. | $\frac{5}{13}$ | C. | -2016 | D. | -$\frac{2}{3}$ |
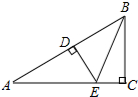 如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.