��Ŀ����
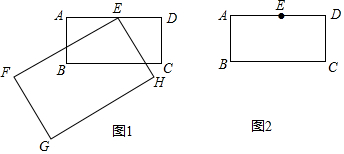
11�� ��ͼ����ƽ��ֱ������ϵxOy�У���A�ӵ�O��ʼ��x����������ƶ�����B�ڡ�xOyƽ�������ƶ����ƶ��б���AB=2���䣬��ABΪһ�ߣ���AB�Ҳ�������ABCD����BC=1��
��ͼ����ƽ��ֱ������ϵxOy�У���A�ӵ�O��ʼ��x����������ƶ�����B�ڡ�xOyƽ�������ƶ����ƶ��б���AB=2���䣬��ABΪһ�ߣ���AB�Ҳ�������ABCD����BC=1����1����AB��OAʱ�������OC�ij���
��2��ȡAB���е�E����O��E��C���㹲��ʱ�������OA��OC�ij���
��3�����OAB�����Բ�뾶ΪR�����ж����ƶ�������R��ֵ�Ƿ����仯�������䣬�����R��ֵ�����仯����˵�����ɣ�
��4����ֱ��д���߶�OC�����ֵ��
���� ��1����AB��OA�����OD��CD�ij��ȣ�Ȼ�����ù��ɶ����������OC�ij��ȣ�
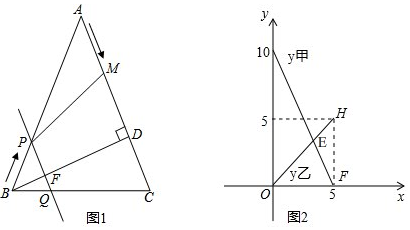
��2����O��E��C���㹲��ʱ����ͼ��ʾ������E��EF��OB�ڵ�F������C��CG��OB�ڵ�G������A��AH��OB�ڵ�H����֤����BFE�ա�BCG��AAS�����Ӷ���֪��CG=x��BG=y���ֿ�֪��OEF�ס�OCG���Ӷ������x��y��ֵ�����������������ε����ʼ������OC�������õ��������ε����ʼ������OA��ֵ��
��3�����OAB�����ԲM������BM���ӳ�����M��N������AN���Ӷ���֪��BOA=��BNA=45�㣬��BAN=90�㣬����BN=$\sqrt{2}$AB��
��4���ֱ���A��BΪԲ�ģ�ABΪ�뾶��Բ����ԲA��OB��ԲB��OA����ʱ��OC�����ֵ����ʱ������������OC�ij��ȣ�Ȼ���ٽ��бȽϼ��ɣ�
���  �⣺��1����AB��OAʱ��
�⣺��1����AB��OAʱ��
�ߡ�BOA=45�㣬
��OA=AB=2��
��AD=BC=1��
��OD=OA+AD=3��
�ɹ��ɶ�����֪��OC=$\sqrt{9+4}$=$\sqrt{13}$��
��2����O��E��C���㹲��ʱ����ͼ��ʾ��
����E��EF��OB�ڵ�F������C��CG��OB�ڵ�G������A��AH��OB�ڵ�H��
��CG=x��BG=y��
��E��AB���е㣬
��BE=BC=1��
�ߡ�ABC=90�㣬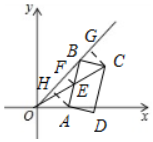
���FBE+��CBG=��CBG+��BCG=90�㣬
���FBE=��BCG��
�ڡ�BFE���BCG�У�
$\left\{\begin{array}{l}{��FBE=��BCG}\\{��EFB=��BGC}\\{BE=BC}\end{array}\right.$
���BFE�ա�BCG��AAS��
��EF=BG=y��BF=CG=x��
��E��AB���е㣬EF��AH��
��AH=2FE=2y��
�ߡ�AOB=45�㣬
��OH=AH=2y��
��EF��CG��
���OEF�ס�OCG��
$\frac{EF}{CG}$=$\frac{OF}{OG}$��
��$\frac{y}{x}$=$\frac{2y+x}{2x+3y}$��
��x2=3y2��
��Rt��BEF�У��ɹ��ɶ�����֪��
x2+y2=1��
��4y2=1��
��y=$\frac{1}{2}$��y=-$\frac{1}{2}$���ᣩ
��x=$\frac{\sqrt{3}}{2}$��
��OG=2x+3y=$\sqrt{3}$+$\frac{3}{2}$��CG=$\frac{\sqrt{3}}{2}$��
��Rt��BEC��
��CE=$\sqrt{2}$��
��$\frac{EF}{CG}$=$\frac{OE}{OC}$��
��$\frac{y}{x}=\frac{OE}{OE+\sqrt{2}}$��
��OE=$\frac{\sqrt{6}+\sqrt{2}}{2}$��
��OC=OE+CE=$\frac{\sqrt{6}+3\sqrt{2}}{2}$
��OA=$\sqrt{2}$OH=2$\sqrt{2}$y��
��OA=$\sqrt{2}$��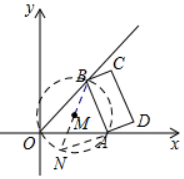
��3�����OAB�����ԲM��
����BM���ӳ�����M��N������AN��
��$\widehat{AB}=\widehat{AB}$��
���BOA=��BNA=45�㣬
��BN�ǡ�M��
���BAN=90�㣬
��BN=$\sqrt{2}$AB=2$\sqrt{2}$��
��R=$\sqrt{2}$
���ƶ�������R��ֵ���ᷢ���仯��
��4����BΪԲ�ģ�ABΪ�뾶����B��
����B��OA����ʱ��
��ʱAB��OA��
�ɣ�1����֪��OC=$\sqrt{13}$��
��AΪԲ�ģ�ABΪ�뾶����B��
����A��OB����ʱ��
��ʱAB��OB��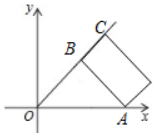
��AB=OB=2��
��OC=OB+BC=3��
��$\sqrt{13}$��3��
���߶�OC�����ֵΪ$\sqrt{13}$
���� ���⿼��Բ���ۺ����⣬�漰ȫ�������ε��������ж������������ε��������ж����ⷽ�̣����ɶ��������ߵ����ʣ�����ֱ�������ε����ʵ�֪ʶ���ۺϳ̶Ƚϸߣ���Ҫѧ�����������ѧ֪ʶ��

| A�� | xy��0 | B�� | $\frac{x}{y}$��0 | C�� | x+y��0 | D�� | x-y��0 |
 ��ͼ��OA��OC��OB��OD����λͬѧ�ֱ�˵���Լ��Ĺ۵㣮�ף���AOB=��COD���ң���BOC+��AOD=180�㣬������AOB���COD���ǡ�BOC����ǣ�����ͼ��С��ƽ�ǵĽ���4����������ȷ�Ľ����У�������
��ͼ��OA��OC��OB��OD����λͬѧ�ֱ�˵���Լ��Ĺ۵㣮�ף���AOB=��COD���ң���BOC+��AOD=180�㣬������AOB���COD���ǡ�BOC����ǣ�����ͼ��С��ƽ�ǵĽ���4����������ȷ�Ľ����У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
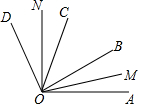 ��ͼ����֪����OM��ON�ֱ�ƽ�֡�AOB����COD������MON=������BOC=�£����AOD=��������
��ͼ����֪����OM��ON�ֱ�ƽ�֡�AOB����COD������MON=������BOC=�£����AOD=��������| A�� | 2�� | B�� | 2��-�� | C�� | ��+�� | D�� | ��-�� |
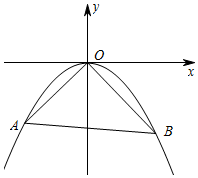 ��ͼ��ֱ��y=kx+b��b��0����������y=ax2�ཻ�ڵ�A��x1��y1����B��x2��y2�����㣬������y=ax2�����㣨4��-2��
��ͼ��ֱ��y=kx+b��b��0����������y=ax2�ཻ�ڵ�A��x1��y1����B��x2��y2�����㣬������y=ax2�����㣨4��-2��