题目内容
1.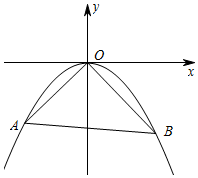 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)(1)求出a的值;
(2)若x1•OB-y2•OA=0,求b的值;
(3)将抛物线向右平移一个单位,再向上平移n的单位.若在第一象限的抛物线上存在这样的不同的两点M、N,使得M、N关于直线y=x对称,求n的取值范围.
分析 (1)利用待定系数法即可解决问题.
(2)作AE⊥x轴于E,BF⊥x轴于F.首先证明△OAE∽△BOF,推出∠AOB=90°,由$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{8}{x}^{2}}\end{array}\right.$,消去y得到x2+8kx+8b=0,推出x1x2=8b,y1y2=-$\frac{1}{8}$x12•(-$\frac{1}{8}$x22)=$\frac{1}{64}$(x1x2)2=b2,由OA2+OB2=AB2,推出x12+y12+x22+y22=(x1-x2)2+(y1-y2)2,可得-2x1x2-2y1y2=0,即-16b-2b2=0,解方程即可解决问题.
(3)设平移后的抛物线的解析式为y=-$\frac{1}{8}$(x-1)2+n,直线MN的解析式为y=-x+m,由$\left\{\begin{array}{l}{y=-\frac{1}{8}(x-1)^{2}+n}\\{y=-x+m}\end{array}\right.$消去y得到x2-10x+8m-8n+1=0,由M、N关于直线y=x对称,可得5=$\frac{m}{2}$,推出m=10,推出x2-10x+81-8n=0,由题意△>0,可得100-4(81-8n)>0,解不等式即可解决问题.
解答 解:(1)∵抛物线y=ax2经过点(4,-2),
∴-2=a×42,得a=-$\frac{1}{8}$,即a的值是-$\frac{1}{8}$;
(2)作AE⊥x轴于E,BF⊥x轴于F.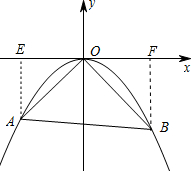
由题意OE=-x1,BF=-y2,
∵x1•OB-y2•OA=0,
∴OE•OB=BF•OA,
∴$\frac{OE}{BF}$=$\frac{OA}{OB}$,
∴△OAE∽△BOF,
∴∠AOE=∠OBF,
∵∠OBF+∠BOF=90°,
∴∠AOE+∠BOF=90°,
∴∠AOB=90°,
由$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{8}{x}^{2}}\end{array}\right.$,消去y得到x2+8kx+8b=0,
∴x1x2=8b,y1y2=-$\frac{1}{8}$x12•(-$\frac{1}{8}$x22)=$\frac{1}{64}$(x1x2)2=b2,
∵OA2+OB2=AB2,
∴x12+y12+x22+y22=(x1-x2)2+(y1-y2)2,
∴-2x1x2-2y1y2=0,
∴-16b-2b2=0,
解得b=-8或0(舍弃),
∴b=-8.
(3)设平移后的抛物线的解析式为y=-$\frac{1}{8}$(x-1)2+n,直线MN的解析式为y=-x+m,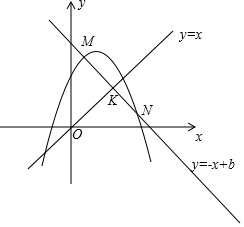
直线y=-x+m与直线y=x的交点为K,则K($\frac{m}{2}$,$\frac{m}{2}$),
由$\left\{\begin{array}{l}{y=-\frac{1}{8}(x-1)^{2}+n}\\{y=-x+m}\end{array}\right.$消去y得到x2-10x+8m-8n+1=0,
∵M、N关于直线y=x对称,
∴5=$\frac{m}{2}$,
∴m=10,
∴x2-10x+81-8n=0,
由题意△>0,
∴100-4(81-8n)>0,
解得n>7.
点评 本题考查二次函数综合题、一次函数的性质、相似三角形的判定和性质、直角三角形的判定和性质、勾股定理、一元二次方程的根的判别式等知识,解题的关键是灵活应用所学知识解决问题,学会利用参数解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
 如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.
如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.
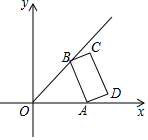 如图,在平面直角坐标系xOy中,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,移动中保持AB=2不变,以AB为一边,着AB右侧作矩形ABCD,且BC=1.
如图,在平面直角坐标系xOy中,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,移动中保持AB=2不变,以AB为一边,着AB右侧作矩形ABCD,且BC=1.