题目内容
4.某课外活动小组为了了解本校学生上网目的,随机调查了本校的部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图:根据以上信息解答下列问题: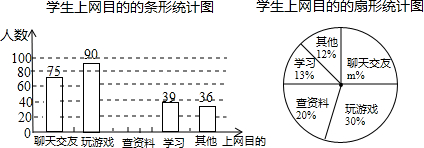
(1)参与本次调查的学生共有300人;
(2)在扇形统计图中,m的值为25;
(3)补全条形统计图;
(4)中学生上网玩游戏、聊天交友已经对正常的学习产生较多负面影响,为此学校计划开展一次“合理上网”专题讲座,每班随机抽取15名学生参加,小明所在的班级有50名学生,他被抽到听讲座的概率是多少?
分析 (1)根据:玩游戏人数÷玩游戏的百分比=总人数,计算可得;
(2)根据:聊天交友人数÷总人数×100可得m的值;
(3)总人数×查资料的百分比可得人数,补全条形图即可;
(4)用抽取人数除以班级总人数可得概率.
解答 解:(1)90÷30%=300(人);
(2)m=$\frac{75}{300}$×100=25;
(3)300×20%=60(人),补全图形如下:
(4)小明被抽到听讲座的概率是$\frac{15}{50}$=$\frac{3}{10}$.
故答案为:(1)300,(2)25.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
14. 如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
 如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | 4 | D. | 6 |
13.一元二次方程x2-2x-1=0,其解的情况正确的是( )
| A. | 有两个相等的实数解 | B. | 有两个不相等的实数解 | ||
| C. | 没有实数解 | D. | 不确定 |
14.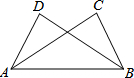 如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
 如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )| A. | ∠D=∠C | B. | BD=AC | C. | ∠CAD=∠DBC | D. | AD=BC |
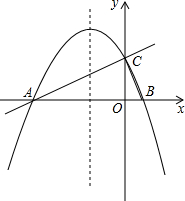 已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.
已知抛物线的解析式为y=-$\frac{1}{2}{x^2}-\frac{3}{2}$x+c.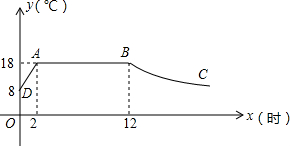 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解析下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解析下列问题: 如图所示,将一个含60°角的直角三角形按照如图放置在作业纸上,纸上横线是一组平行线,若∠1=20°,则∠2=50°.
如图所示,将一个含60°角的直角三角形按照如图放置在作业纸上,纸上横线是一组平行线,若∠1=20°,则∠2=50°.