题目内容
16．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}\\{x+2y=4}\end{array}\right.$的解满足x+y$＞-\frac{3}{2}$，求满足条件的m的取值范围为m＜$\frac{7}{2}$．分析 方程组两方程相加表示出x+y，代入已知不等式求出解集即可确定出m的范围．
解答 解：$\left\{\begin{array}{l}{2x+y=-3m+2①}\\{x+2y=4②}\end{array}\right.$，
①+②得：3（x+y）=-3m+6，即x+y=-m+2，
代入不等式得：-m+2＞-$\frac{3}{2}$，
解得：m＜$\frac{7}{2}$，
故答案为：m＜$\frac{7}{2}$
点评 此题考查了二元一次方程组的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
7．八名学生参加初中英语听力口语自动化考试成绩如下：28，21，29，27，30，26，30，25．这组数据的平均数、极差分别是（ ）
| A． | 26、9 | B． | 27、9 | C． | 27、10 | D． | 28、10 |
8．
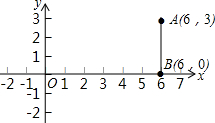如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O为位似中心，相似比为$\frac{1}{3}$，在第一象限内把线段AB缩小后得到新的线段，则点A的对应点坐标为（ ）
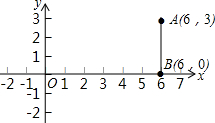如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O为位似中心，相似比为$\frac{1}{3}$，在第一象限内把线段AB缩小后得到新的线段，则点A的对应点坐标为（ ）| A． | （2，1） | B． | （2，0） | C． | （3，3） | D． | （3，1） |
5．
“描点法”作图是探究函数图象的基本方法，小明同学用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
根据表格上的信息回答问题：
（1）二次函数y=ax2+bx+c与y轴交点坐标是（0，1）；该抛物线的开口向下；当x=4时，二次函数y=ax2+bx+c的值为-3
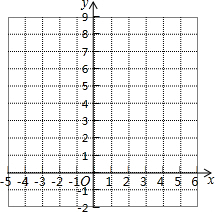
（2）小明还用“描点法”研究了函数y=$\frac{4}{{x}^{2}}$的图象和性质，请你在下面的方格纸中帮小明画出函数y=$\frac{4}{{x}^{2}}$的图象．借助所画的图象，回答下面问题：
①函数y=$\frac{4}{{x}^{2}}$的图象关于y轴对称；
②当x＞0时，y随x的增大而增大；当x＜0时，y随x的增大而减小．
“描点法”作图是探究函数图象的基本方法，小明同学用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
（1）二次函数y=ax2+bx+c与y轴交点坐标是（0，1）；该抛物线的开口向下；当x=4时，二次函数y=ax2+bx+c的值为-3
（2）小明还用“描点法”研究了函数y=$\frac{4}{{x}^{2}}$的图象和性质，请你在下面的方格纸中帮小明画出函数y=$\frac{4}{{x}^{2}}$的图象．借助所画的图象，回答下面问题：
①函数y=$\frac{4}{{x}^{2}}$的图象关于y轴对称；
②当x＞0时，y随x的增大而增大；当x＜0时，y随x的增大而减小．
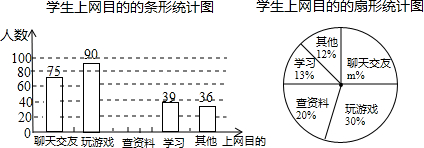
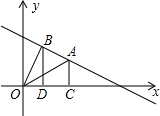如图，一次函数y=-$\frac{1}{2}$x+3的图象上有两点A、B，A点的横坐标为3，B点的横坐标为a（0＜a＜6且a≠3），过点A、B分别作x轴的垂线，垂足为C、D，△AOC、△BOD的面积分别为S1，S2，则S1，S2的大小关系是（ ）