题目内容
14. 如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )
如图,边长为$\frac{5}{4}$的正方形ABCD的顶点A在y轴上,顶点D在反比例函数$y=\frac{k}{x}(x>0)$的图象上,已知点B的坐标是$({\frac{3}{4},\frac{9}{4}})$,则k的值为( )| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | 4 | D. | 6 |
分析 如图,作DE⊥OA于E,BF⊥OA于F,证明△ADE≌△BAF,在RT△ABF中,利用勾股定理即可解决问题.
解答 解:如图,作DE⊥OA于E,BF⊥OA于F,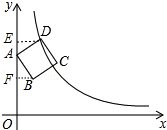
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∵∠EAD+∠FAB=90°,∠FAB+∠ABF=90°,
∴∠EAD=∠ABF,
在△ADE和△BAF中,
$\left\{\begin{array}{l}{∠DEA=∠BFA=90°}\\{∠EAD=∠ABF}\\{DA=AB}\end{array}\right.$,
∴△ADE≌△BAF,
∴AF=ED,AE=BF,
∵B点坐标($\frac{3}{4}$,$\frac{9}{4}$),AB=$\frac{5}{4}$,
∴OF=$\frac{9}{4}$,AF=DE=$\sqrt{A{B}^{2}-F{B}^{2}}$=$\sqrt{(\frac{5}{4})^{2}-(\frac{3}{4})^{2}}$=1.
∴OE=4,点D坐标(1,4),
∴k=4.
故选C.
点评 本题考查反比例函数的有关知识,正方形的性质,全等三角形的判定和性质,解决问题的关键是构造全等三角形,属于中考常考题型.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
5.若实数x、y满足$\sqrt{2x-1}+|{y-1}|=0$,则x+y的值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
2.若a-b=3,ab=1,则a2+b2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
19.若$\sqrt{(a-2)^{2}}$=2-a,则a的值( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
3. 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
 如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )
如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F恰好为DC的中点,DG⊥AE,垂足为G.若DG=3,则AE的边长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 16 |