题目内容
8.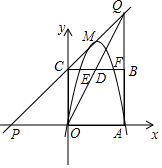 如图,抛物线y=-x2+2mx(m>1)交x轴于点O,A,顶点为M,以OA为边向上方作正方形OABC,直线CM交x轴于点P,交直线AB于点Q,连接OQ交直线BC于点D,
如图,抛物线y=-x2+2mx(m>1)交x轴于点O,A,顶点为M,以OA为边向上方作正方形OABC,直线CM交x轴于点P,交直线AB于点Q,连接OQ交直线BC于点D,(1)当点M在BC的上方时,线段BC交抛物线于点E,F(点E在点F的左侧),
①若EF=CE+BF,求m的值;
②若CP=OQ,求证:△OCD≌△CBQ;
(2)记点A关于OQ的对称点为A′,是否存在m,使得A'落在抛物线的对称轴上?若存在,求出m的值;若不存在,请说明理由.
分析 (1)①用m的代数式表示点E的坐标,利用待定系数法即可角问题;
②首先证明Rt△PCO≌Rt△QOA,推出∠CPO=∠OQA,由OC∥AQ,BC∥AP,推出∠COD=∠AQO,∠CPO=∠QCB,推出∠QCB=∠COD,由此即可证明;
(2)存在.如图1中,连接A′Q,作A′N⊥AB于N.首先证明△OAA′是等边三角形,再求出直线CM的解析式,可得点Q坐标,想办法列出方程即可解决问题;
解答 (1)①解:由题意A(2m,0),C(0,2m),B(2m,2m),
由对称性可知CE=BF,
∵EF=CE+BF,
∴CE=$\frac{1}{4}$BC,
∴E($\frac{1}{2}$m,2m),把E点坐标代入y=-x2+2mx得到2m=-$\frac{1}{4}$m2+m2,解得m=$\frac{8}{3}$或0(舍弃)
∴m=$\frac{8}{3}$.
②证明:如图,
在Rt△PCO和Rt△QOA中,
$\left\{\begin{array}{l}{PC=OQ}\\{OC=OA}\end{array}\right.$,
∴Rt△PCO≌Rt△QOA,
∴∠CPO=∠OQA,
∵OC∥AQ,BC∥AP,
∴∠COD=∠AQO,∠CPO=∠QCB,
∴∠QCB=∠COD,
在△OCD和△CBQ中,
$\left\{\begin{array}{l}{∠COD=∠QCB}\\{OC=BC}\\{∠OCD=∠CBQ}\end{array}\right.$,
∴△OCD≌△CBQ;
(2)存在.理由如下:
如图1中,连接A′Q,作A′N⊥AB于N.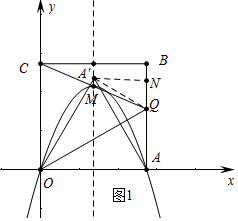
由题意OA=OA′=AA′,
∴△OAA′是等边三角形,
∴∠AOQ=∠QOA′=30°,
∴∠A′QN=∠A′QO=∠AQO=60°,
∵C(0,2m),M(m,m2),
∴直线CM的解析式为y=(m-2)x+2m,
令x=2m,得到y=2m2-2m,
∴Q(2m,2m2--2m),
在Rt△A′QN中,A′N=A′Q•cos30°,
∴(2m2-2m)•$\frac{\sqrt{3}}{2}$=m,
∴m=$\frac{3+\sqrt{3}}{3}$或0(舍弃),
∴满足条件的m的值为$\frac{3+\sqrt{3}}{3}$.
点评 本题考查二次函数综合题、待定系数法、正方形的性质、锐角三角函数、全等三角形的判定和性质等知识,解题的关键是灵活应用所学知识解决问题,最后一个问题的突破点是发现等边三角形解决问题,学会构建方程,用方程的思想思考问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,AB∥CD,直线l交AB于点E,交CD于F点,若∠1=70°,则∠2的度数为( )
如图,AB∥CD,直线l交AB于点E,交CD于F点,若∠1=70°,则∠2的度数为( )| A. | 20° | B. | 70° | C. | 110° | D. | 160° |
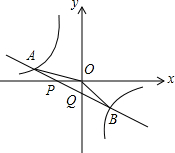 如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b>$\frac{{k}_{2}}{x}$的解集在x<-2或0<x<1,其中正确的结论是( )
如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+$\frac{1}{2}$n=0;③S△AOP=S△BOQ;④不等式k1x+b>$\frac{{k}_{2}}{x}$的解集在x<-2或0<x<1,其中正确的结论是( ) 如图,已知等边三角形ABC,D是AB边上一点,作DE⊥AB交AC于点F,交BC延长线于点E,求证:CE=CF.
如图,已知等边三角形ABC,D是AB边上一点,作DE⊥AB交AC于点F,交BC延长线于点E,求证:CE=CF.