题目内容
10.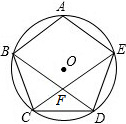 如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
分析 根据圆心角、弧、弦的关系定理和正多边形的性质计算即可.
解答 解:∵$\widehat{BC}$=$\widehat{CD}$,
∴BC=CD,
∴△BCD是等腰三角形,
同理,△CDE是等腰三角形,
∵$\widehat{BC}$=$\widehat{AE}$=$\widehat{AB}$,
∴∠BCE=∠AEC=72°,
∴∠FCD=108°-72°=36°,
同理,∠FDC=36°,
∴∠FCD=∠FDC,
∴FC=FD,
∴△FCD是等腰三角形,
∠BCF=∠BFC=72°,
∴△BCF是等腰三角形,
同理△EFD是等腰三角形,
∴图中有5个等腰三角形,
故答案为:5.
点评 本题考查的是圆心角、弧、弦的关系、等腰三角形的判定,掌握在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
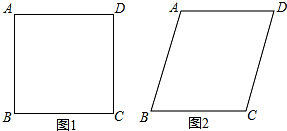
20.如图,将四根长度相等的细木条首尾相接钉成四边形ABCD,当∠B=90°时,测得AC=4,改变它的形状使∠B=60°,此时AC的长度为( )

| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
20.已知关于x的方程x2-2x-m=0有两个不相等的实数根,则m的取值范围为( )
| A. | m<0 | B. | m<-2 | C. | m≥0 | D. | m>-1 |
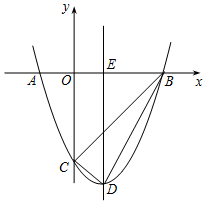 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
 如图,⊙O是△ABC的外接圆,∠BOC=136°,则∠A的大小是68°.
如图,⊙O是△ABC的外接圆,∠BOC=136°,则∠A的大小是68°.