题目内容
2.如果关于x的不等式组$\left\{\begin{array}{l}{2(a-x)≥-x-4}\\{\frac{3x+4}{2}<x+1}\end{array}\right.$的解集为x<-2,且使关于x的分式方程$\frac{x}{x-3}$+$\frac{a+2}{3-x}$=2的解为非负数的所有整数a的个数为( )| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
分析 把a看做已知数表示出不等式组的解,根据已知解集确定出a的范围,分式方程去分母转化为整式方程,将a的整数解代入整式方程,检验分式方程解为负分数确定出所有a的值即可.
解答 解:$\left\{\begin{array}{l}{2(a-x)≥-x-4①}\\{\frac{3x+4}{2}<x+1②}\end{array}\right.$,
由①得:x≤2a+4,
由②得:x<-2,
由不等式组的解集为x<-2,得到2a+4≥-2,即a≥-3,
分式方程去分母得:a-3x-3=1-x,
解分式方程$\frac{x}{x-3}$+$\frac{a+2}{3-x}$=2,
两边同时乘(x-3),可得x-a-2=2(x-3),解得x=4-a,
但当a=1时,x=3,不符合题意,舍去,
∵分式方程$\frac{x}{x-3}$+$\frac{a+2}{3-x}$=2的解为非负数,
∴4-a≥0,
∴-3≤a≤4且a≠1,
∴符合题意的a的值有7个,
故选A.
点评 本题主要考查了解一元一次不等式组以及解分式方程,由不等式组和分式方程求得a的取值范围是解题的关键,注意分式方程中x≠3.

练习册系列答案
相关题目
17.下列各项中,结论正确的是( )
| A. | 若a>0,b<0,则$\frac{b}{a}$>0 | B. | 若a>b,则a-b>0 | ||
| C. | 若a<0,b<0,则ab<0 | D. | 若a>b,a<0,则$\frac{b}{a}$<0 |
7.若x>y,则下列式子错误的是( )
| A. | x-2>y-2 | B. | x+1>y+1 | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | -5x>-5y |
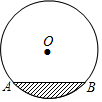 如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.
如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.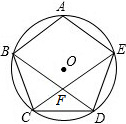 如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.