题目内容
1.解方程:(1)2(3x-5)-3(4x-3)=0;
(2)$\frac{2x+1}{3}$-$\frac{10x+1}{6}$=1.
(3)y-$\frac{1}{2}$(y-1)=$\frac{2}{3}$(y-1);
(4)$\frac{0.2-x}{0.3}$-1=$\frac{0.1+x}{0.2}$.
分析 (1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可;
(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
(3)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
(4)先利用分数的基本性质整理,再去分母,去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.
解答 解:(1)去括号得,6x-10-12x+9=0,
移项得,6x-12x=10-9,
合并同类项得,-6x=1,
系数化为1得,x=-$\frac{1}{6}$;
(2)去分母得,2(2x+1)-(10x+1)=6,
去括号得,4x+2-10x-1=6,
移项得,4x-10x=6-2+1,
合并同类项得,-6x=5,
系数化为1得,x=-$\frac{5}{6}$;
(3)去分母得,6y-3(y-1)=4(y-1),
去括号得,6y-3y+3=4y-4,
移项得,6y-3y-4y=-4-3,
合并同类项得,-y=-7,
系数化为1得,y=7;
(4)方程可化为,$\frac{2-10x}{3}$-1=$\frac{1+10x}{2}$,
去分母得,2(2-10x)-6=3(1+10x),
去括号得,4-20x-6=3+30x,
移项得,-20x-30x=3-4+6,
合并同类项得,-50x=5,
系数化为1得,x=-$\frac{1}{10}$.
点评 本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
9. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )| A. | 32 | B. | 24 | C. | 16 | D. | 8 |
6.体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设应邀请x队参加比赛,则可列方程为( )
| A. | x(x+1)=28 | B. | x(x-1)=28 | C. | $\frac{1}{2}$x(x+1)=28 | D. | $\frac{1}{2}$x(x-1)=28 |
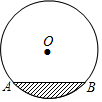 如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.
如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.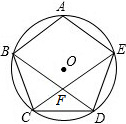 如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.