题目内容
18.等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为80°,50°,130°.分析 等腰三角形一腰上的高与底边的夹角为40°,根据直角三角形两锐角互余求出底角的度数,再根据等腰三角形两底角相等列式进行计算即可得解.
等腰三角形一腰上的高与另一腰的夹角为40°,首先根据题意画出图形,一种情况等腰三角形为锐角三角形,即可推出顶角的度数为50°.另一种情况等腰三角形为钝角三角形,由题意,即可推出顶角的度数为130°.
解答 解:如图,
∵一腰上的高与底边的夹角为40°,
∴底角∠C=90°-40°=50°,
∴顶角∠A=180°-2×50°=180°-100°=80°.
故答案为:80°.如图,等腰三角形为锐角三角形,
∵BD⊥AC,∠ABD=40°,
∴∠A=50°,
即顶角的度数为50°.
如图,等腰三角形为钝角三角形,
∵BD⊥AC,∠DBA=40°,
∴∠BAD=50°,
∴∠BAC=130°.
故答案为:80°,50°,130°.
点评 本题考查了等腰三角形两底角相等的性质,直角三角形两锐角互余的性质,需要注意等腰三角形一腰上的高与底边的夹角为40°中等腰三角形是钝角三角形时不成立.此题难度适中,解题的关键在于正确的画出图形,结合图形,利用数形结合思想求解.

练习册系列答案
相关题目
9. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )| A. | 32 | B. | 24 | C. | 16 | D. | 8 |
6.体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设应邀请x队参加比赛,则可列方程为( )
| A. | x(x+1)=28 | B. | x(x-1)=28 | C. | $\frac{1}{2}$x(x+1)=28 | D. | $\frac{1}{2}$x(x-1)=28 |
3.关于x的不等式x-b≥0恰有两个负整数解,则b的取值范围是( )
| A. | -3<b<-2 | B. | -3<b≤-2 | C. | -3≤b≤-2 | D. | -3≤b<-2 |
7.若x>y,则下列式子错误的是( )
| A. | x-2>y-2 | B. | x+1>y+1 | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | -5x>-5y |
8.已知关于x的一元二次方程x2+kx+k=0的一根是-2,则另一根x=( )
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
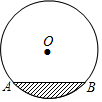 如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.
如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.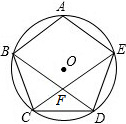 如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.