题目内容
20．计算：$\sqrt{2{x}^{3}}$•$\sqrt{\frac{1}{{x}^{2}y}}$（x＞0，y＞0）分析 直接利用二次根式的性质化简求出即可．
解答 解：$\sqrt{2{x}^{3}}$•$\sqrt{\frac{1}{{x}^{2}y}}$（x＞0，y＞0）
=$\sqrt{2{x}^{3}×\frac{1}{{x}^{2}y}}$
=$\sqrt{2xy}$．
点评 此题主要考查了二次根式的乘除运算，正确化简二次根式是解题关键．
练习册系列答案
相关题目
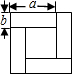用4张全等的长方形拼成一个如图所示的正方形，利用面积的不同表示方法可以写出一个代数恒等式．若长方形的长和宽分别为a、b，则该图可表示的代数恒等式是4ab=（a+b）2-（a-b）2．．
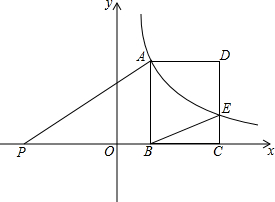如图，矩形ABCD中，AB=3，BC=2，点A在反比例函数y=$\frac{k}{x}$（x＞0），图象上点E是双曲线与CD的交点．点B，C和点P（-5，0）均在x轴上，PA∥BE．
12．若直线l与直线y=2x-3关于x轴对称，则直线l的解析式为（ ）
| A． | y=-2x-3 | B． | y=-2x+3 | C． | y=$\frac{1}{2}$x+3 | D． | y=-$\frac{1}{2}$x-3 |
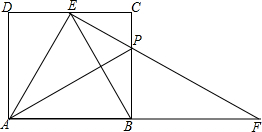如图，在矩形ABCD中，AB=2，AD=$\sqrt{3}$，在边CD上有一点E，使EB平分∠AEC．若P为BC边上一点，且BP=2CP，连接EP并延长交AB的延长线于F．给出以下五个结论：