题目内容
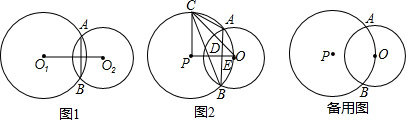
5.如果两个圆有两个不同的公共点,我们就称这两个圆相交.如图1已知知⊙O1和⊙O2相交于A、B两点,我们就称线段AB是⊙O1和⊙O2的公共弦.(1)求证:两圆圆心的连线O1O2垂直平分公共弦AB;
(2)如图2,⊙P与⊙O相交于点A、B,并且⊙P经过点O,点C是⊙P的优弧AB上任意一点(不与点A、B重合),弦OC交公共弦AB于点D,连结CA、CB.
①求证:CO平分∠ACB;
②当点C在⊙P上什么位置时,直线CA与⊙O相切?并说明理由;
③当∠ACB等于60°时,两圆的半径有什么关系?并说明理由.
分析 (1)先判断出点O1在线段AB的垂直平分线上,同理:O2也在线段AB的垂直平分线上,即可得出结论;
(2)①判断出$\widehat{OA}=\widehat{OB}$,即可得出结论;
②延长与⊙P交于点F.若点C在点F位置时,直线CA与⊙O相切,然后根据直径所对的圆周角是直角可得∠OAF=90°,进而得到OA⊥FA,即FA与⊙O相切;
③当∠ACB=60°时,两圆半径相等,作直径OF,连接BF,AF,OA,然后证明∠AFO=30°,再根据直角三角形中,30°角所对的直角边等于斜边的一半可得OA=$\frac{1}{2}$OF,进而得到OP=OA.
解答 解:(1)如图1,
连接O1A,O1B,O2A,O2B,
∴O1A=O1B,
∴点O1在线段AB的垂直平分线上,
同理:O2在线段AB的垂直平分线上,
∴O1O2是线段AB的垂直平分线,
两圆圆心的连线O1O2垂直平分公共弦AB;
(2)①同(1)的方法得出PO垂直平分AB,
∴$\widehat{OA}=\widehat{OB}$,
∴∠OCA=∠OCB,
∴CO平分∠ACB;
②解:如图2,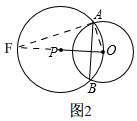 延长与⊙P交于点F.
延长与⊙P交于点F.
若点C在点F位置时,直线CA与⊙O相切,
理由:连接AF,
∵FO是⊙P的直径,
∴∠FAO=90°,
∴OA⊥FA,
∴FA与⊙O相切,
即点C在点F位置时,直线CA与⊙O相切.
③如图3,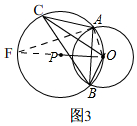 当∠ACB=60°时,两圆半径相等.理由:
当∠ACB=60°时,两圆半径相等.理由:
解:作直径OF,连接BF,AF,OA,
∵∠AFB=∠ACB=60°,PO垂直平分AB,
∴$\widehat{AO}=\widehat{BO}$,
∴∠AFO=∠BEO,
∴∠AFO=30°,
∵OF是直径,
∴∠FAO=90°,
∴OA=$\frac{1}{2}$OF,
∴OA=PO,
∴当∠ACB=60°时,两圆半径相等.
点评 此题是圆的综合题,主要考查了线段的垂直平分线的判定和性质,角平分线的性质,切线的判定,含30度角的直角三角形的性质,解(1)的关键是判断出点O1在线段AB的垂直平分线上,解(2)的关键是判断出∠FAO=90°,是一道中等难度的中考常考题.

 某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
s12=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70
计算高中队决赛成绩的方差s22;
(3)从统计学的角度分析,你认为哪个决赛成绩较好,说明你的理由.
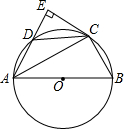 已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.
已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.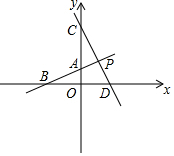 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.