题目内容
17. 某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
s12=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70
计算高中队决赛成绩的方差s22;
(3)从统计学的角度分析,你认为哪个决赛成绩较好,说明你的理由.
分析 (1)根据条形统计图可以计算出初中部的平均分和众数以及高中部的中位数;
(2)根据表格中的数据,可以结合两队成绩的平均数和中位数,说明哪个队的决赛成绩较好;
(3)根据它们的方差,从而可以解答本题.
解答 解:(1)由条形统计图可得,
初中5名选手的平均分是:$\frac{75+80+85+85+100}{5}$=85,众数是85,中位数是85,
高中五名选手的成绩是:70,75,80,100,100,故中位数是80,
故答案为:85,85,85,80;
(2)S${{\;}_{2}}^{2}$=$\frac{1}{5}$[(70-85)2+(75-85)2+(80-85)2+(100-85)2+(100-85)2]=160,
(3)由题意可得,s12=70,s22=160
∵70<160,
故初中部代表队选手成绩比较稳定.
点评 本题考查条形统计图、加权平均数、众数、中位数、方差,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列计算错误的是( )
| A. | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$ | B. | $\frac{a-1}{b-1}$=$\frac{a}{b}$ | C. | $\frac{a-b}{b-a}$=-1 | D. | $\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$ |
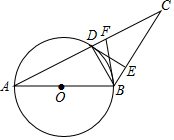 如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
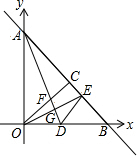 如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.