题目内容
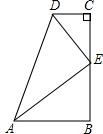 如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由.
如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由.考点:全等三角形的判定与性质
专题:
分析:首先延长DE交AB的延长线于点F,由∠B=∠C=90°,E是BC的中点,易证得△DCE≌△FBE,得出DE=EF,CD=BF,又有AE⊥DE,即可证得AD=AF,进而即可求得AD=CD+AB.
解答:解:AD=CD+AB;
理由:延长DE交AB的延长线于点F,
∵∠B=∠C=90°,E是BC的中点,
∴∠C=∠EBF=90°,CE=BE,
在△CDE和△BFE中,
,
∴△DCE≌△FBE(ASA),
∴DE=EF,DC=BF,
∵AE⊥DE,
∴AD=AF,
∴AD=AB+BF=AB+DC,
即AD=CD+AB.
理由:延长DE交AB的延长线于点F,
∵∠B=∠C=90°,E是BC的中点,
∴∠C=∠EBF=90°,CE=BE,
在△CDE和△BFE中,
|
∴△DCE≌△FBE(ASA),
∴DE=EF,DC=BF,
∵AE⊥DE,
∴AD=AF,
∴AD=AB+BF=AB+DC,
即AD=CD+AB.
点评:此题考查了角平分线的性质、全等三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
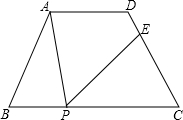 如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.
如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长. 如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC.
如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC. 如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标.
如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标.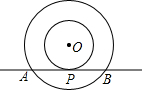 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.