题目内容
已知在△ABC中,BC=120mm,边BC上的高为80mm,在这个三角形内有一个内接矩形,矩形的一边在BC上,另两个顶点分别在边AB、AC上.问当这个矩形面积最大时,它的边长各是多少?
考点:相似三角形的判定与性质,二次函数的最值,矩形的性质
专题:常规题型
分析:设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
解答:解:设PN=x(mm),

由条件可得△APN∽△ABC,
∴
=
,
即
=
,
解得PQ=80-
x.
∴S=PN•PQ=x(80-
x)=-
x2+80x=-
(x-60)2+2400,
∴S的最大值为2400mm2,
此时PN=60mm,
PQ=80-
×60=40(mm).

由条件可得△APN∽△ABC,
∴
| PN |
| BC |
| AE |
| AD |
即
| x |
| 120 |
| 80-PQ |
| 80 |
解得PQ=80-
| 2 |
| 3 |
∴S=PN•PQ=x(80-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴S的最大值为2400mm2,
此时PN=60mm,
PQ=80-
| 2 |
| 3 |
点评:本题考查了相似三角形的应用,二次函数的最值问题,根据相似三角形对应高的比等于对应边的比列式表示出正方形的边长与三角形的边与这边上的高的关系是解题的关键,此题规律性较强,是道好题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
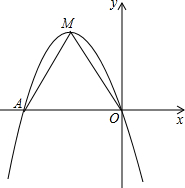 已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′.
已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′.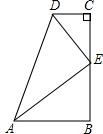 如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由.
如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由. 如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.
如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB. 一圆柱高9cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是
一圆柱高9cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是