题目内容
在直角坐标平面内,点O在坐标原点,已知点A(3,1)、B(2,0)、C(4,-2).
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
考点:相似三角形的判定与性质,坐标与图形性质
专题:常规题型
分析:(1)分别求AB,OB,BC的长即可求得
=
,即可判定;
(2)根据相似三角形对应角相等即可解题.
| AB |
| OB |
| OB |
| BC |
(2)根据相似三角形对应角相等即可解题.
解答:解:如图:

(1)∵A(3,1)、B(2,0)、C(4,-2).
∴AB=
,BC=2
,OB=2,
=
,
∵∠ABx=∠CBx=45°,
∴∠ABO=∠CBO=135°,
∴△AOB∽△OCB.
(2)∵△AOB∽△OCB.
∴∠BOC=∠A,
∵∠AOC=∠AOB+∠BOC=∠AOB+∠A,
∴∠AOC=45°.

(1)∵A(3,1)、B(2,0)、C(4,-2).
∴AB=
| 2 |
| 2 |
| AB |
| OB |
| OB |
| BC |
∵∠ABx=∠CBx=45°,
∴∠ABO=∠CBO=135°,
∴△AOB∽△OCB.
(2)∵△AOB∽△OCB.
∴∠BOC=∠A,
∵∠AOC=∠AOB+∠BOC=∠AOB+∠A,
∴∠AOC=45°.
点评:本题考查了相似三角形的判定,考查了相似三角形对应角相等的性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,等边△ABC中,点M在AC边上,点N在CB的延长线上,且AM=BN,MC=nAM,线段MN交AB交于P点.
如图,等边△ABC中,点M在AC边上,点N在CB的延长线上,且AM=BN,MC=nAM,线段MN交AB交于P点.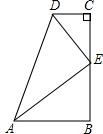 如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由.
如图,在数学活动课上,李明提出这样一个问题:∠B=∠C=90°,E是BC的中点,且AE⊥DE,则线段AD、CD、AB之间的数量关系是什么?请说明理由.