题目内容
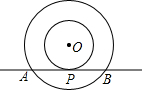如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点．求证：AP=BP．考点：切线的性质,垂径定理
专题：证明题
分析：根据切线的性质得出OP⊥AB，根据垂径定理得出即可．
解答：证明：如图，连接OP，
∵大圆的弦AB是小圆的切线，点P为切点，
∴OP⊥AB，
∵OP过O，
∴AP=BP．
∵大圆的弦AB是小圆的切线，点P为切点，
∴OP⊥AB，
∵OP过O，
∴AP=BP．
点评：本题考查了切线的性质和垂径定理的应用，主要考查学生的推理能力，题目比较好，难度适中．
练习册系列答案
相关题目
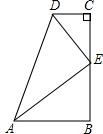如图，在数学活动课上，李明提出这样一个问题：∠B=∠C=90°，E是BC的中点，且AE⊥DE，则线段AD、CD、AB之间的数量关系是什么？请说明理由．
在13×13的网格中，已知△ABC和点M（1，2）．
如图，四边形ABCD中，∠B+∠D=180°，AB=AD，∠BAD=60°，S四边形ABCD=在☉O中
=2
，则弦AB与弦CD的大小关系是（ ）
 |
| AB |
|
| CD |
| A、AB＞2CD |
| B、AB=2CD |
| C、AB＜2CD |
| D、AB=CD |