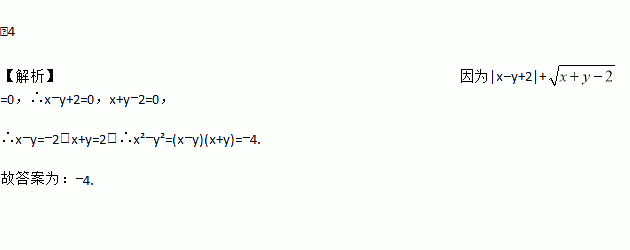题目内容
已知|x﹣y+2|+
=0，则x2﹣y2的值为______．
﹣4
【解析】因为|x?y+2|+=0，∴x?y+2=0，x+y?2=0，
∴x?y=?2，x+y=2，∴x²?y²=(x?y)(x+y)=?4.
故答案为：?4.
练习册系列答案
阅读快车系列答案
相关题目
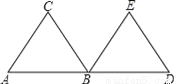
如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．由一个三角形变换到另一个三角形（ ）
A. 仅能由平移得到
B. 仅能由旋转得到
C. 既能由平移得到，也能由旋转得到
D. 既不能由平移得到，也不能由旋转得到
C
【解析】【解析】
∵△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．
∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．故选C． 已知：如图，在△ABC中有D、E两点，求证：BD＋DE＋EC＜AB＋AC．
见解析
【解析】试题分析：延长BD交AC于M点，延长CE交BD的延长线于点N．在△ABM中，AB+AM>BM，在△CNM中，NM+MC>NC，所以AB+AM+NM+MC>BM+NC，再由AM+MC=AC，BM=BN+NM可知AB+AC+NM>BN+NM+NC，故AB+AC>BN+NC，在△BNC中，BN+NC=BD+DN+NE+EC，在△DNE中，DN+NE>DE，由此即可得出结论．
... 已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
C
【解析】试题解析：∵∠A+∠B+∠C=180°，∠B+∠C=∠A，
∴2∠A=180°，
∴∠A=90°，
即△ABC一定是直角三角形；
故选C． 如图，在一块边长为a的正方形纸板四周，各剪去一个边长为b(b＜0)的正方形．
(1)用代数式表示阴影部分的面积；
(2)利用因式分解的方法计算当a＝15.4，b＝3.7时，阴影部分的面积．
(1) a2－4b²;(2) 182.4.
【解析】试题分析：
试题解析：（1）用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积；（2）把所得的代数式用平方差公式因式分解后，代入求值即可.
(1)S阴影＝a2－4b2；
(2)S阴影＝(a＋2b)(a－2b)＝(15.4＋2×3.7)(15.4－2×3.7)＝22.8×8＝182.4. 分解因式：16－x2＝( )
A. (4－x)(4＋x) B. (x－4)(x＋4)
C. (8＋x)(8－x) D. (4－x)2
A
【解析】试题分析：直接利用平方差公式分解因式得出答案．16﹣x2=（4﹣x）（4+x）． 已知函数y=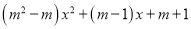
(1)若这个函数是一次函数，求m的值;
(2)若这个函数是二次函数，则m的值应怎样？
(1)、m=0；(2)、m≠0且m≠1.
【解析】试题分析：（1）由一次函数的定义求解；
（2）由二次函数的定义求解．
试题解析：（1）由一次函数的定义，得： ，解得m=0或m=1，又∵m﹣1≠0即m≠1；∴当m=0时，这个函数是一次函数；
（2）由二次函数的定义，得： ，解得且，∴当且时，这个函数是二次函数． 已知二次函数y=2x2+bx﹣1．
（1）求证：无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）若两点P（﹣3，m）和Q（1，m）在该函数图象上．
①求b、m的值；
②将二次函数图象向上平移多少单位长度后，得到的函数图象与x轴只有一个公共点？
（1）无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）b=4，m=5；（3）二次函数图象向上平移3个单位
【解析】
试题分析：（1）先计算判别式的值，再利用非负数的性质可判断△=＞0，然后根据判别式的意义可判断抛物线与x轴必有两个交点；
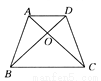
（2）①先利用抛物线的对称性可确定抛物线的对称轴方程，从而可求出b的值，然后计算自变量为1所对应的函数值即可得... 如图所示，在四边形ABCD中，已知AB与 CD不平行，∠ABD＝∠ACD，请你添加一个条件：______ ，使的加上这个条件后能够推出AD∥BC ，且AB＝CD．
∠DAC＝∠ADB或∠BAD＝∠CDA或∠DBC＝∠ACB或∠ABC＝∠DCB或OB＝OC或OA＝OD.
【解析】试题分析：先证四边形AECO是梯形，再说明是等腰梯形．由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA，同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=C...