题目内容
16.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )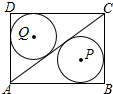
| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2$\sqrt{2}$ |
分析 根据矩形的性质可得出⊙P和⊙Q的半径相等,利用直角三角形内切圆半径公式即可求出⊙P半径r的长度.连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,求出线段QE、EP的长,再由勾股定理即可求出线段PQ的长,此题得解.
解答 解:∵四边形ABCD为矩形,
∴△ACD≌△CAB,
∴⊙P和⊙Q的半径相等.
在Rt△ABC中,AB=4,BC=3,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∴⊙P的半径r=$\frac{AB+BC-AC}{2}$=$\frac{3+4-5}{2}$=1.
连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,则∠QEP=90°,如图所示.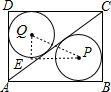
在Rt△QEP中,QE=BC-2r=3-2=1,EP=AB-2r=4-2=2,
∴PQ=$\sqrt{Q{E}^{2}+E{P}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故选B.
点评 本题考查了三角形的内切圆与内心、矩形的性质以及勾股定理,解题的关键是求出⊙P和⊙Q的半径.本题属于中档题,难度不大,解决该题时,巧妙的借用了直角三角形内切圆的半径公式求出了⊙P和⊙Q的半径.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
4.下列事件是随机事件的是( )
| A. | 购买一张福利彩票,中特等奖 | |
| B. | 在一个标准大气压下,加热水到100℃,沸腾 | |
| C. | 任意三角形的内角和为180° | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
8.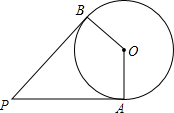 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )| A. | $\frac{2}{3}$π | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
5.不等式组$\left\{\begin{array}{l}{x-3<1}\\{3x+2≤4x}\end{array}\right.$的解集为( )
| A. | x≤2 | B. | x<4 | C. | 2≤x<4 | D. | x≥2 |
18.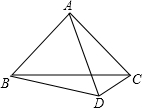 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )| A. | 30° | B. | 15° | C. | 45° | D. | 35° |