题目内容
8．
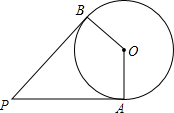如图，PA、PB是⊙O的切线，切点分别为A、B，若OA=2，∠P=60°，则$\widehat{AB}$的长为（ ）| A． | $\frac{2}{3}$π | B． | π | C． | $\frac{4}{3}π$ | D． | $\frac{5}{3}π$ |
分析 由PA与PB为圆的两条切线，利用切线的性质得到两个角为直角，再利用四边形内角和定理求出∠AOB的度数，利用弧长公式求出$\widehat{AB}$的长即可．
解答 解：∵PA、PB是⊙O的切线，
∴∠OBP=∠OAP=90°，
在四边形APBO中，∠P=60°，
∴∠AOB=120°，
∵OA=2，
∴$\widehat{AB}$的长l=$\frac{120π×2}{180}$=$\frac{4}{3}$π，
故选C
点评 此题考查了弧长的计算，以及切线的性质，熟练掌握弧长公式是解本题的关键．
练习册系列答案
相关题目
16．如图，矩形ABCD中，AB=4，BC=3，连接AC，⊙P和⊙Q分别是△ABC和△ADC的内切圆，则PQ的长是（ ）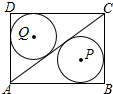
| A． | $\frac{5}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | 2$\sqrt{2}$ |
如图，在四边形ABCD中，∠ABC=30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，若AB=3，BC=4，则BD=5（提示：可连接BE）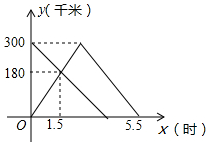
甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示．
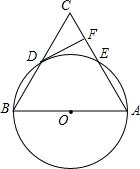如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F．
9．在有理数-3，-1$\frac{1}{2}$，0.3，-1，-96，5.9中，整数有（ ）
| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
10．
如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（ ）
如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B．下列结论中不一定成立的是（ ）| A． | PA=PB | B． | PO平分∠APB | C． | AB垂直平分OP | D． | ∠OBA=∠OAB |