题目内容
1．A、B两地相距200千米，甲车从A地出发匀速开往B地，乙车同时从B地出发匀速开往A地，两车相遇时距A地80千米．已知乙车每小时比甲车多行驶30千米，求甲、乙两车的速度．分析 根据题意，可以设出甲、乙的速度，然后根据题目中的关系，列出相应的方程，本题得以解决．
解答 解：设甲车的速度是x千米/时，乙车的速度为（x+30）千米/时，
$\frac{80}{x}=\frac{200-80}{x+30}$
解得，x=60，
经检验，x=60是分式方程的根，
则x+30=90，
即甲车的速度是60千米/时，乙车的速度是90千米/时．
点评 本题考查分式方程的应用，解题的关键是明确题意，找出所求问题需要的条件，发现题目中的数量关系，列出相应的方程．
练习册系列答案
相关题目
11．若△ABC≌△A′B′C′，且AB=AC=9，△ABC的周长为26cm，则B′C′的长为（ ）
| A． | 10cm | B． | 9cm | C． | 4cm | D． | 8cm |
如图，在△ABC中，AB=BC=4，S△ABC=4$\sqrt{3}$，点P、Q、K分别为线段AB、BC、AC上任意一点，则PK+QK的最小值为2$\sqrt{3}$．
16．如图，矩形ABCD中，AB=4，BC=3，连接AC，⊙P和⊙Q分别是△ABC和△ADC的内切圆，则PQ的长是（ ）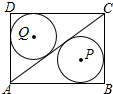
| A． | $\frac{5}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | 2$\sqrt{2}$ |
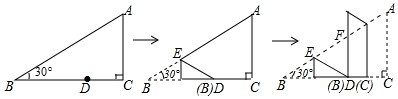
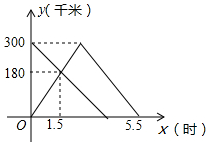甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示．
3．在反比例函数y=-$\frac{2}{x}$的图象上有两点（-$\frac{1}{2}$，y1），（-2，y2），则y1-y2的值是（ ）
| A． | 正数 | B． | 负数 | C． | 非正数 | D． | 不能确定 |