题目内容
18.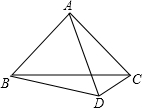 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )| A. | 30° | B. | 15° | C. | 45° | D. | 35° |
分析 由等腰直角三角形的性质得出∠BAC=90°,∠ACB=45°,AB=AC,求出∠DAC=30°,由等腰三角形的性质和三角形内角和定理求出∠ACD=75°,即可得出∠BCD.
解答 解:∵△ABC是等腰直角三角形,
∴∠BAC=90°,∠ACB=45°,AB=AC,
∵∠BAD=60°,且AD=AB,
∴∠DAC=90°-60°=30°,AD=AC,
∴∠ACD=∠ADC=(180°-30°)÷2=75°,
∴∠BCD=∠ACD-∠ACB=75°-45°=30°;
故选:A.
点评 本题考查了等腰直角三角形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握等腰直角三角形的性质,由等腰三角形的性质和三角形内角和定理求出∠ACD是解决问题的关键.

练习册系列答案
相关题目
16.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )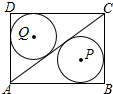

| A. | $\frac{5}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2$\sqrt{2}$ |
9.在有理数-3,-1$\frac{1}{2}$,0.3,-1,-96,5.9中,整数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
6.我们知道:31=3,32=9,33=27,34=81,35=243…;81=8,82=64,83=512,84=4096,85=32768…,那么1282015+632016结果的个位数字是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
13.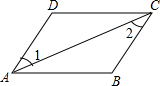 如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
 如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )| A. | 两直线平行,内错角相等 | B. | 两直线平行,同位角相等 | ||
| C. | 内错角相等,两直线平行 | D. | 同位角相等,两直线平行 |
3.在反比例函数y=-$\frac{2}{x}$的图象上有两点(-$\frac{1}{2}$,y1),(-2,y2),则y1-y2的值是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 不能确定 |
10. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )| A. | PA=PB | B. | PO平分∠APB | C. | AB垂直平分OP | D. | ∠OBA=∠OAB |
8.为了建设节约型社会,鼓励居民节约用水,志愿小组在社区宣传时,随机对该社区10户居民的月用水量进行了调查,下表是这10户居民2016年4月份用水量的调查结果:
则这10户居民用水量的中位数为( )
| 居民户数 | 1 | 5 | 3 | 1 |
| 月用水量(米3/户) | 10 | 15 | 20 | 25 |
| A. | 15 | B. | 17.5 | C. | 20 | D. | 20 |
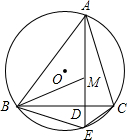 如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.
如图,点M是△ABC的内心,AM的延长线交边BC于点D,交△ABC外接圆⊙O于点E,连接BE、CE.