题目内容
3. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.
如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.
分析 根据AB∥CD判断出∠1=∠C=45°,根据∠3是△ECD的外角,判断出∠3=∠C+∠2,从而求出∠3的度数.
解答 解:∵AB∥CD
∴∠1=∠C=45°,
∵∠3是△ECD的外角,
∴∠3=∠C+∠2,
∴∠3=45°+35°=80°.
点评 本题考查了平行线的性质和三角形的外角的性质,灵活运用是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知$\frac{1}{x}-\frac{1}{y}=2$,则$\frac{2}{y^2}+\frac{2y-4x}{{{x^2}y}}$的值是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 8 | D. | $\frac{1}{8}$ |
8. 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
 如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )
如图,将正方体的平面展开图重新折成正方体后,“快”字对面的字是( )| A. | 新 | B. | 年 | C. | 祝 | D. | 乐 |
15. 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )
 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )| A. | -3 | B. | -2 | C. | -2.5 | D. | -3.5 |
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高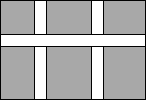 如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽.
如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽. 如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3.
如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3.