题目内容
12. 如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3.
如图,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,若BD=3,则DE=3.
分析 根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°,根据等角对等边得出DE=BD=3.
解答 解:∵△ABC为等边三角形,BD是AC边的中线,
∴BD⊥AC,BD平分∠ABC,∠DBE=$\frac{1}{2}$∠ABC=30°.
∵CD=CE,
∴∠CDE=∠E.
∵∠ACB=60°,且∠ACB为△CDE的外角,
∴∠CDE+∠E=60°.
∴∠CDE=∠E=30°,
∴∠DBE=∠DEB=30°,
∴DE=BD=3.
故答案为3.
点评 本题考查了等腰三角形的判定与性质及等边三角形的性质;此题把等边三角形的性质和等腰三角形的判定结合求解.考查了学生综合运用数学知识的能力,得到∠E=30°是正确解答本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.下列各数中,有理数是( )
| A. | $\sqrt{5}$ | B. | $\frac{π}{3}$ | ||
| C. | $\frac{1}{2}$ | D. | 3.03003000300003… |
17.判断一元二次方程x2-2x+1=0的根的情况是( )
| A. | 只有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
4. 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )| A. | AB=$\frac{1}{3}$AC | B. | EC=2BD | C. | B是AE的中点 | D. | DE=$\frac{2}{3}$AB |
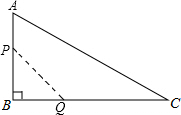 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.
如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.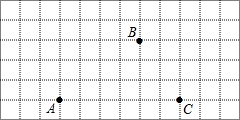 如图,A、B、C是网格图中的三点.
如图,A、B、C是网格图中的三点.