题目内容
18.已知抛物线$y=-\frac{1}{2}{x^2}-x+4$,则:(1)x取何值时,y随x增大而减小?
(2)x取何值时,抛物线在x轴上方?
分析 (1)根据抛物线的性质,抛物线开口向下,在对称轴的右侧,y的值随x值的增大而减小,即可得出x的取值范围;
(2)令y=0,确定函数图象与x轴的交点,结合开口方向判断x的取值范围.
解答 解:(1)∵$y=-\frac{1}{2}{x^2}-x+4$,
∴抛物线对称轴是直线x=$\frac{1}{2×(-\frac{1}{2})}$=-1,开口向下,
∴当x>-1时,y随x增大而减小;
(2)当y=0时,即-$\frac{1}{2}$x2-x+4=0,
解得x1=2,x2=-4,
∵抛物线开口向下,
∴当-4<x<2时,抛物线在x轴上方.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是直线x=-$\frac{b}{2a}$.当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.也考查了抛物线与x轴的交点.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
7.下列各数中,有理数是( )
| A. | $\sqrt{5}$ | B. | $\frac{π}{3}$ | ||
| C. | $\frac{1}{2}$ | D. | 3.03003000300003… |
8.比较2$\sqrt{2}$,3,$\sqrt{7}$的大小,正确的是( )
| A. | $\sqrt{7}$<3<2$\sqrt{2}$ | B. | 2$\sqrt{2}$<$\sqrt{7}$<3 | C. | $\sqrt{7}$<2$\sqrt{2}$<3 | D. | 2$\sqrt{2}$<3<$\sqrt{7}$ |
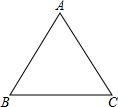 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.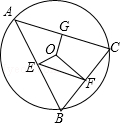 如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.
如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.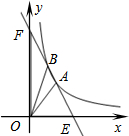 如图,直线y=-2x+b与双曲线y=$\frac{3}{x}$(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF+S△OAE=4S△AOB,则b的值是5.
如图,直线y=-2x+b与双曲线y=$\frac{3}{x}$(x>0)交于A,B两点,与x轴、y轴分别交于E,F两点,连结OA,OB,若S△OBF+S△OAE=4S△AOB,则b的值是5. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数.
如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,求∠3的度数. 如图,已知点O在线段AB上,点C、D分别是AO、BO的中点
如图,已知点O在线段AB上,点C、D分别是AO、BO的中点