题目内容
11.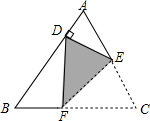 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
分析 首先由折叠得出DE=CE,利用等边△ABC和∠ADE=90°,AD=2,得出AE=4,利用勾股定理得出DE,即可求得AC的长.
解答 解:∵将等边△ABC折叠,使得点C落在AB边上的点D处,
∴DE=CE,∠A=60°,
∵∠ADE=90°,AD=2,
∴AE=2AD=4,
∴DE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴AC=AE+CE=AE+DE=4+2$\sqrt{3}$.
故选:D.
点评 此题考查折叠的性质,勾股定理,含30°角直角三角形的性质,等边三角形的性质,找出相等的边,转化问题是解决问题的关键.

练习册系列答案
相关题目
1.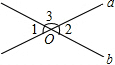 如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
 如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )| A. | 50°,40° | B. | 50°,130° | C. | 130°,50° | D. | 50°,50° |
19.在下列各组的条件中,不能判定△ABC和△DEF全等的是( )
| A. | AB=DE,∠B=∠E,∠C=∠F | B. | AC=DF,BC=DE,∠C=∠D | ||
| C. | AB=EF,∠A=∠E,∠B=∠F | D. | ∠A=∠F,∠B=∠E,AC=DE |
16.若分式$\frac{x-1}{x+2}$的值为0,则x的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 0 |
1.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |