题目内容
20．若$\sqrt{1-3a}$和|8b-3|互为相反数，则$\frac{1}{ab}$的立方根是2．分析 根据非负数的性质求出a、b的值，计算得到$\frac{1}{ab}$的值，根据立方根的概念得到答案．
解答 解：由题意得，$\sqrt{1-3a}$+|8b-3|=0，
∴1-3a=0，8b-3=0，
解得，a=$\frac{1}{3}$，b=$\frac{3}{8}$，
$\frac{1}{ab}$=8，
8的立方根是2，
∴$\frac{1}{ab}$的立方根是2，
故答案为：2．
点评 本题考查的是非负数的性质，掌握几个非负数的和为0时，这几个非负数都为0是解题的关键．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
11．
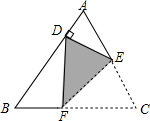如图，将等边△ABC折叠，使得点C落在AB边上的点D处，若∠ADE=90°，AD=2，则AC的长为（ ）
如图，将等边△ABC折叠，使得点C落在AB边上的点D处，若∠ADE=90°，AD=2，则AC的长为（ ）| A． | 4 | B． | 8 | C． | 4$\sqrt{3}$ | D． | 4+2$\sqrt{3}$ |
8．
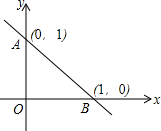如图一次函数y=kx+b的图象与y轴交于点（0，1），与x轴交于点（1，0），则关于x的不等式kx+b＞1的解集是（ ）
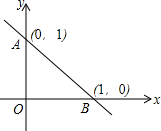如图一次函数y=kx+b的图象与y轴交于点（0，1），与x轴交于点（1，0），则关于x的不等式kx+b＞1的解集是（ ）| A． | x＞0 | B． | x＜0 | C． | x＞1 | D． | x＜1 |
5．筷子中有同样大小的红球1个、绿球2个，随机提出1个小球记下颜色后放回，再随机摸出1个，则两次摸到的球都是绿球的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{9}$ |
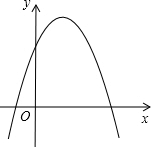二次函数y=ax2+bx+c（a≠0）的图象如图所示，则：a＜0；b＞0；c＞0；b2-4ac＞0．