题目内容
2.已知抛物线y=(x-1)2-4的顶点为(1,-4).①将它沿直线y=$\frac{1}{2}$翻折,求翻折后的顶点坐标;
②将它沿直线y=-$\frac{3}{2}$翻折,求翻折后的顶点坐标.
分析 ①顶点(1,-4)沿直线y=$\frac{1}{2}$翻折后的点的纵坐标不变;
②顶点(1,-4)沿直线y=-$\frac{3}{2}$翻折后的点的纵坐标不变.
解答 解:①设点(1,-4)沿直线y=$\frac{1}{2}$翻折后的点的坐标为(1,-y),
则$\frac{-4+y}{2}$=$\frac{1}{2}$,
解得y=5,
则顶点(1,-4)沿直线y=$\frac{1}{2}$翻折后的顶点坐标是(1,5);
②设点(1,-4)沿直线y=-$\frac{3}{2}$翻折后的点的坐标为(1,y),
则$\frac{-4+y}{2}$=-$\frac{3}{2}$,
解得x=1,
则顶点(1,-4)沿直线y=-$\frac{3}{2}$翻折后的顶点坐标是(1,1).
点评 本题考查了二次函数图象与几何变换.熟知关于直线对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
11.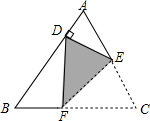 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
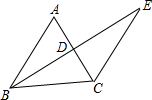 如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.
如图,BE⊥AC于点D,且AD=CD,BD=ED,若∠A=54°,求∠E的度数.