题目内容
19.在下列各组的条件中,不能判定△ABC和△DEF全等的是( )| A. | AB=DE,∠B=∠E,∠C=∠F | B. | AC=DF,BC=DE,∠C=∠D | ||
| C. | AB=EF,∠A=∠E,∠B=∠F | D. | ∠A=∠F,∠B=∠E,AC=DE |
分析 根据“AAS”对A进行判断;根据“SAS”对B进行判断;根据“ASA”对C进行判断;当∠A=∠F,∠B=∠E时,AC与DE不是对应边,所以可对D进行判断.
解答 解:A、若AB=DE,∠B=∠E,∠C=∠F,则△ABC≌△DEF(AAS),所以A选项错误;
B、若AC=DF,BC=DE,∠C=∠D,则△ABC≌△FED(SAS),所以B选项错误;
C、若AB=EF,∠A=∠E,∠B=∠F,则△ABC≌△EFD(ASA),所以C选项错误;
D、若∠A=∠F,∠B=∠E,AC=DF,则△ABC≌△EFD(ASA),所以D选项正确.
故选D.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
11.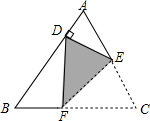 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
8.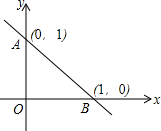 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
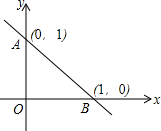 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
 母亲节那天,很多同学给妈妈准备了鲜花和礼盒.
母亲节那天,很多同学给妈妈准备了鲜花和礼盒.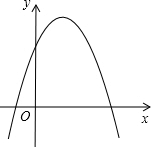 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.