题目内容
1.如图,二次函数y=ax2-2ax-3a(a<0)的图象与x轴交于A,B两点(点B在点A的右侧),与y轴的正半轴交于点C,顶点为D.若以BD为直径的⊙M经过点C.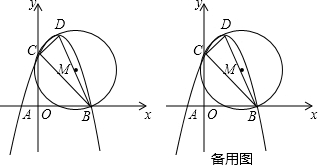
(1)请直接写出C,D的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)⊙M上是否存在点E,使得∠EDB=∠CBD?若存在,请求出所满足的条件的E的坐标;若不存在,请说明理由.
分析 (1)计算横坐标为0的函数值即可得到C点坐标,然后将解析式配成顶点式即可得出点D的坐标;
(2)先利用二次函数与x轴的交点问题确定A点和B点坐标,再根据圆周角定理得到∠BCD=90°,则根据两点间的距离公式得BC2=9a2+9,CD2=a2+1,BD2=16a2+4,接着利用勾股定理得到9a2+9+a2+1=16a2+4,然后解方程求出a即可得到二次函数解析式;
(3)先计算出CD2=2,BC2=18,再根据圆周角定理,由∠EDB=∠CBD得弧CD=弧BE,则CD=BE,接着证明Rt△BED≌Rt△DCB,得到DE=BC,设E(x,y),根据两点间的距离公式得(x-1)2+(y-4)2=18,(x-3)2+y2=2,然后解方程组得x=4,y=1或x=$\frac{8}{5}$,y=-$\frac{1}{5}$,从而可得满足条件的E点坐标.
解答 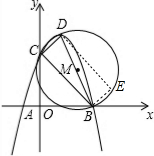 解:(1)当x=0时,ax2-2ax-3a-3a,则点C的坐标为(0,-3a);
解:(1)当x=0时,ax2-2ax-3a-3a,则点C的坐标为(0,-3a);
∵y=ax2-2ax-3a=a(x-1)2-4a,
∴点D的坐标为(1,-4a);
(2)当y=0时,ax2-2ax-3a=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
∵BD为⊙M的直径,
∴∠BCD=90°,
而BC2=(0-3)2+(-3a-0)2=9a2+9,CD2=(0-1)2+(-3a+4a)2=a2+1,BD2=(3-1)2+(0+4a)2=16a2+4,
在Rt△BCD中,∵BC2+CD2=BD2,
∴9a2+9+a2+1=16a2+4,
整理得a2=1,解得a1=-1,a2=1(舍去);
∴抛物线解析式为:y=-x2+2x+3;
(3)存在.
a=1,CD2=a2+1=2,BC2=9a2+9=18,
∵∠EDB=∠CBD,
∴CD=BE,
而BD为直径,
∴∠BED=90°,
∴Rt△BED≌Rt△DCB,
∴DE=BC,
设E(x,y),
∴ED2=(x-1)2+(y-4)2,BE2=(x-3)2+y2,
∴(x-1)2+(y-4)2=18,(x-3)2+y2=2,
解得x=4,y=1或x=$\frac{8}{5}$,y=-$\frac{1}{5}$,
∴满足条件的E点坐标为(4,1)、($\frac{8}{5}$,-$\frac{1}{5}$).
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数与x轴的交点问题和圆周角定理;理解坐标与图形性质,会利用两点间的距离公式计算线段的长.

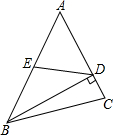 如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.
如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于8.
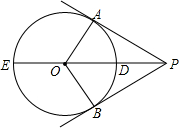 如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.
如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.