题目内容
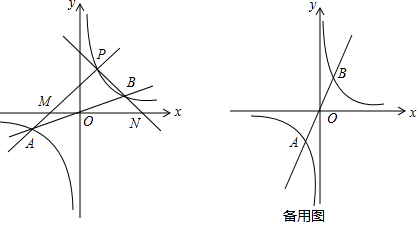
17.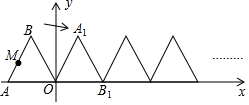 如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是(5,$\sqrt{3}$),翻滚2017次后AB中点M经过的路径长为($\frac{1346\sqrt{3}}{3}$+896)π.
如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是(5,$\sqrt{3}$),翻滚2017次后AB中点M经过的路径长为($\frac{1346\sqrt{3}}{3}$+896)π.
分析 如图作B3E⊥x轴于E,易知OE=5,B3E=$\sqrt{3}$,观察图象可知3三次一个循环,一个循环点M的运动路径为$\frac{120•π•\sqrt{3}}{180}$+$\frac{120π•1}{180}$+$\frac{120π•1}{180}$=($\frac{2\sqrt{3}+4}{3}$)π,由2017÷3=672…1,可知翻滚2017次后AB中点M经过的路径长为672•($\frac{2\sqrt{3}+4}{3}$)π+$\frac{2\sqrt{3}}{3}$π=($\frac{1346\sqrt{3}}{3}$+896)π.
解答 解: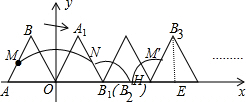 如图作B3E⊥x轴于E,易知OE=5,B3E=$\sqrt{3}$,
如图作B3E⊥x轴于E,易知OE=5,B3E=$\sqrt{3}$,
∴B3(5,$\sqrt{3}$),
观察图象可知3三次一个循环,一个循环点M的运动路径为$\frac{120•π•\sqrt{3}}{180}$+$\frac{120π•1}{180}$+$\frac{120π•1}{180}$=($\frac{2\sqrt{3}+4}{3}$)π,
∵2017÷3=672…1,
∴翻滚2017次后AB中点M经过的路径长为672•($\frac{2\sqrt{3}+4}{3}$)π+$\frac{2\sqrt{3}}{3}$π=($\frac{1346\sqrt{3}}{3}$+896)π.
故答案为($\frac{1346\sqrt{3}}{3}$+896)π.
点评 本题考查轨迹、规律题、弧长公式、等边三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,循环从特殊到一般的探究方法,属于中考常考题型.

练习册系列答案
相关题目
8. 关于右面两个几何体的视图,正确的说法是( )
关于右面两个几何体的视图,正确的说法是( )
 关于右面两个几何体的视图,正确的说法是( )
关于右面两个几何体的视图,正确的说法是( )| A. | 它们的主视图相同 | B. | 它们的俯视图相同 | ||
| C. | 它们的左视图不同 | D. | 它们的三种视图均不同 |
7.下列几何体中,主视图、俯视图、左视图都相同的是( )
| A. | 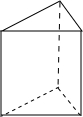 | B. |  | C. |  | D. |  |
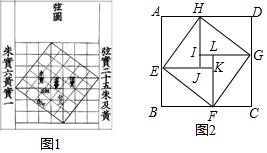
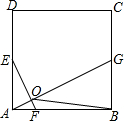 如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=$\frac{1}{4}$AB.
如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=$\frac{1}{4}$AB.