题目内容
5.已知x=2002,y=-1,n为自然数,求代数式(x2n+y2n+xnyn)(xn-yn)-(x2n-xnyn)+y2n(xn+yn)的值.分析 先将所求的代数式展开化简,然后根据已知条件讨论n为奇数和偶数,从而可以解答本题.
解答 解:(x2n+y2n+xnyn)(xn-yn)-(x2n-xnyn)+y2n(xn+yn)
=x3n-x2nyn+xny2n-y3n+x2nyn-xny2n-x2n+xnyn+xny2n+y3n
=x3n-x2n+xnyn+xny2n
∵x=2002,y=-1,n为自然数,
∴当n为奇数时,原式=20023n-20022n+2002n×(-1)n+2002n×(-1)2n=20023n-20022n-2002n+2002n=20023n-20022n;
当n为偶数时,原式=20023n-20022n+2002n×(-1)n+2002n×(-1)2n=20023n-20022n+2002n+2002n=20023n-20022n+2×2002n.
点评 本题考查整式的混合运算-化简求值,解题的关键是运用分类讨论的数学思想解答问题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
8.某学校将在体育节举行跳绳活动,为此学校准备购置15米的A种跳绳与3米的B种跳绳若干,已知某商家长、短跳绳的单价如下表
(1)已知购买100条这两种跳绳共花了720元,问A种跳绳买了多少条?
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
| 跳绳种类 | A跳绳 | B跳绳 |
| 单价(单位:元) | 20 | 4 |
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
12. 已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
(1)用函数表达式表示y与x之间的关系;
(2)用表格表示:
(3)用图象表示y与x之间的关系.
 已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
已知两个数的和为10,设其中较大的一个数为x,它们的积为y.(1)用函数表达式表示y与x之间的关系;
(2)用表格表示:
| x | … | ||||||||
| y | … |
10.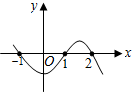 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
 已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )
已知y关于x的函数图象如图所示,则当y<0时,自变量x的取值范围是( )| A. | x<0 | B. | x<-1或1<x<2 | C. | -1<x<1或x>2 | D. | x>-1 |
17.已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( )
| A. | y=x2-2x+2 | B. | y=x2-2x-2 | C. | y=-x2-2x+1 | D. | y=x2-2x+1 |
14.下列具有相反意义的量的是( )
| A. | 上升1米与下降2℃ | B. | 盈利2万元与亏损3万元 | ||
| C. | 气温升高3℃与气温为-3℃ | D. | 体重增加与体重减少 |
15.等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是( )
| A. | 28° | B. | 118° | C. | 62° | D. | 62°或118° |