题目内容
12．
如图，△ABE≌△ACD，点B、D、E、C在一条直线上．（1）∠BAD与∠CAE有何关系？请说明理由．
（2）BD与CE相等吗？为什么？
分析 （1）根据全等三角形的对应角相等解答；
（2）根据全等三角形的对应边相等进行解答．
解答 解：（1）∠BAD=∠CAE，
证明：∵△ABE≌△ACD，
∴∠BAE=∠CAD，
∴∠BAE-∠DAE=∠CAD-∠DAE，
即∠BAD=∠CAE；
（2）∵△ABE≌△ACD，
∴BE=CD，
∴BE-DE=CD-DE，
即BD=CE．
点评 本题考查的是全等三角形性质，掌握全等三角形的对应边相等，全等三角形的对应角相等是解题的关键．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
3．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
下列结论：①c=3；②当x＞1时，y的值随x的增大而减小；③函数的最大值是5；④ac＜0．其中正确的个数为 （ ）
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
7．
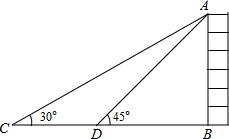如图，某校数学兴趣小组在大厦前的平地上C处，测得大厦顶端A的仰角∠ACB=30°，在D处测得大厦顶端A的仰角∠ADB=45°，那么从点A观察C、D处的视角∠CAD的度数为（ ）
如图，某校数学兴趣小组在大厦前的平地上C处，测得大厦顶端A的仰角∠ACB=30°，在D处测得大厦顶端A的仰角∠ADB=45°，那么从点A观察C、D处的视角∠CAD的度数为（ ）| A． | 60° | B． | 45° | C． | 30° | D． | 15° |
1．已知抛物线y=ax2+bx+c经过原点和第二、三、四象限，则（ ）
| A． | a＞0，b＜0，c=0 | B． | a＜0，b＜0，c=0 | C． | a＞0，b=c=0 | D． | a＜0，b＞0，c=0 |