题目内容
如图,在平面直角坐标系中,抛物线的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交x轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
(1)求抛物线的解析式;
(2)若点D′恰好落在y轴上的点(0,6)时,求此时D点的坐标;
(3)直线CD′交对称轴AB于点F;
①当点D′在对称轴AB的左侧时,且△ED′F∽△CDE,求出DE:DC的值
②连结B D′,是否存在点E,使△E D′B为等腰三角形?若存在,请直接写出BE:BC的值;若不存在请说明理由.
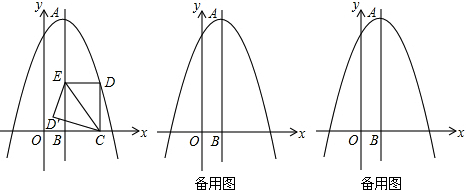
(1)求抛物线的解析式;
(2)若点D′恰好落在y轴上的点(0,6)时,求此时D点的坐标;
(3)直线CD′交对称轴AB于点F;
①当点D′在对称轴AB的左侧时,且△ED′F∽△CDE,求出DE:DC的值
②连结B D′,是否存在点E,使△E D′B为等腰三角形?若存在,请直接写出BE:BC的值;若不存在请说明理由.

考点:二次函数综合题
专题:
分析:(1)先设出抛物线的顶点式,然后根据待定系数法即可求得;
(2)过E点作EF⊥y轴于F,设D的坐标(m,-
(m-3)2+15.),则EF=ED′=m-3,CD′=CD,EF=3,D′O=6,然后根据三角形相似对应边成比例得出关于m的方程,解方程求得m的值即可求得D的坐标;
(3)①根据对折的性质得出∠DCE=∠D′CE,R然后根据平行线和三角形相似即可求得∠D′EF=∠BEC=∠CEB,从而得出∠D′CE=∠DCE=30°,解直角三角形即可求得;②根据等腰三角形的性质,圆周角的性质,得出∠BCD′=∠D′CE=∠BEC,从而得出∠BEC=30°,解直角三角形即可求得;
(2)过E点作EF⊥y轴于F,设D的坐标(m,-
| 1 |
| 5 |
(3)①根据对折的性质得出∠DCE=∠D′CE,R然后根据平行线和三角形相似即可求得∠D′EF=∠BEC=∠CEB,从而得出∠D′CE=∠DCE=30°,解直角三角形即可求得;②根据等腰三角形的性质,圆周角的性质,得出∠BCD′=∠D′CE=∠BEC,从而得出∠BEC=30°,解直角三角形即可求得;
解答: 解:(1)∵抛物线的顶点A的坐标为(3,15),且过点(-2,10),
解:(1)∵抛物线的顶点A的坐标为(3,15),且过点(-2,10),
∴设抛物线的解析式为:y=a(x-3)2+15,
∴10=a(-2-3)2+15,解得:a=-
,
∴抛物线的解析式为:y=-
(x-3)2+15.
(2)如图2,过E点作EF⊥y轴于F,
设D的坐标(m,-
(m-3)2+15.),则EF=ED′=m-3,CD′=CD,EF=3,D′O=6,
∵△EFD′∽△D′OC,
∴
=
,
即:
=
,
整理得:(m-3)2+10(m-3)-75=0,
解得:m=-12(舍去)m=8,
∴D(8,10);

(3)①如图1,根据对折的性质,∠DCE=∠D′CE,
∵DC∥BE,
∴∠DCE=∠BEC,
∵△ED′F∽△CDE,
∴∠D′EF=∠DCE=∠D′CE,
∴∠D′EF=∠BEC=∠CEB,
∵∠D′EF+∠BEC+∠CEB=90°,
∴∠D′CE=∠DCE=30°,
∴
=tan∠DCE=tan30°,
∴DE:DC=
:3.

②如图3,∵△E D′B为等腰三角形,
∴D′E=D′B,
∴∠D′EB=∠D′BE,
∵D′E=BC,
∴D′B=BC,
∠BD′C=∠D′CB,
∵∠EBC=∠ED′C=90°,
∴E、D、′B、C四点共圆,
∴∠D′BE=∠D′CE,∠D′CB=∠D′EB,∠BD′C=∠BEC,
∴∠BCD′=∠D′CE=∠BEC,
∵∠BCD′+∠D′CE+∠BEC=90°,
∴∠BEC=30°,
∴
=cot30°=
,
∴BE:BC=
:1.
 解:(1)∵抛物线的顶点A的坐标为(3,15),且过点(-2,10),
解:(1)∵抛物线的顶点A的坐标为(3,15),且过点(-2,10),∴设抛物线的解析式为:y=a(x-3)2+15,
∴10=a(-2-3)2+15,解得:a=-
| 1 |
| 5 |
∴抛物线的解析式为:y=-
| 1 |
| 5 |
(2)如图2,过E点作EF⊥y轴于F,
设D的坐标(m,-
| 1 |
| 5 |
∵△EFD′∽△D′OC,
∴
| EF |
| D′O |
| ED′ |
| D′C |
即:
| 3 |
| 6 |
| m-3 | ||
-
|
整理得:(m-3)2+10(m-3)-75=0,
解得:m=-12(舍去)m=8,
∴D(8,10);

(3)①如图1,根据对折的性质,∠DCE=∠D′CE,
∵DC∥BE,
∴∠DCE=∠BEC,
∵△ED′F∽△CDE,
∴∠D′EF=∠DCE=∠D′CE,
∴∠D′EF=∠BEC=∠CEB,
∵∠D′EF+∠BEC+∠CEB=90°,
∴∠D′CE=∠DCE=30°,
∴
| DE |
| DC |
∴DE:DC=
| 3 |

②如图3,∵△E D′B为等腰三角形,
∴D′E=D′B,
∴∠D′EB=∠D′BE,
∵D′E=BC,
∴D′B=BC,
∠BD′C=∠D′CB,
∵∠EBC=∠ED′C=90°,
∴E、D、′B、C四点共圆,
∴∠D′BE=∠D′CE,∠D′CB=∠D′EB,∠BD′C=∠BEC,
∴∠BCD′=∠D′CE=∠BEC,
∵∠BCD′+∠D′CE+∠BEC=90°,
∴∠BEC=30°,
∴
| BE |
| BC |
| 3 |
∴BE:BC=
| 3 |
点评:本题考查了待定系数法求解析式,矩形的性质对折的性质,等腰三角形的性质,圆周角的性质,解直角三角形等;

练习册系列答案
相关题目

 如图,已知双曲线y=
如图,已知双曲线y= 如图,已知平行四边形ABCD的BC边在x轴上,A、D两点分别在反比例函数y=-
如图,已知平行四边形ABCD的BC边在x轴上,A、D两点分别在反比例函数y=-