题目内容
翻转类的计算问题在全国各地的中考试卷中出现的频率很大,因此初三(5)班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究.你能和小菲一起解决下列各问题吗?(以下各问只要求写出必要的计算过程和简洁的文字说明即可.)
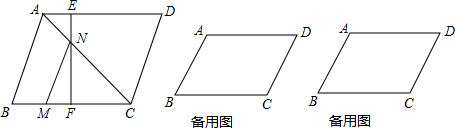
(1)如图①,小菲同学把一个边长为1的正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片向右翻转一周回到初始位置,求顶点O所经过的路程;并求顶点O所经过的路线;
(2)小菲进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片向右翻转若干次.她提出了如下问题:
问题①:若正方形纸片OABC接上述方法翻转一周回到初始位置,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是
π.
(3)①小菲又进行了进一步的拓展研究,若把这个正三角形的一边OA与这个正方形的一边OA重合(如图3),然后让这个正三角形在正方形上翻转,直到正三角形第一次回到初始位置(即OAB的相对位置和初始时一样),求顶点O所经过的总路程.
②若把边长为1的正方形OABC放在边长为1的正五边形OABCD上翻转(如图④),直到正方形第一次回到初始位置,求顶点O所经过的总路程.
(4)规律总结,边长相等的两个正多边形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的 .

(1)如图①,小菲同学把一个边长为1的正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片向右翻转一周回到初始位置,求顶点O所经过的路程;并求顶点O所经过的路线;
(2)小菲进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片向右翻转若干次.她提出了如下问题:
问题①:若正方形纸片OABC接上述方法翻转一周回到初始位置,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是
41+20
| ||
| 2 |
(3)①小菲又进行了进一步的拓展研究,若把这个正三角形的一边OA与这个正方形的一边OA重合(如图3),然后让这个正三角形在正方形上翻转,直到正三角形第一次回到初始位置(即OAB的相对位置和初始时一样),求顶点O所经过的总路程.
②若把边长为1的正方形OABC放在边长为1的正五边形OABCD上翻转(如图④),直到正方形第一次回到初始位置,求顶点O所经过的总路程.
(4)规律总结,边长相等的两个正多边形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的

考点:几何变换综合题
专题:
分析:(1)根据正三角形的性质及弧长公式求出点A绕点B、点C旋转的两段弧长相加即可;
(2)①根据正方形旋转一周的路径,;利用弧长公式以及扇形面积公式求出即可;
②利用正方形纸片OABC经过4次旋转得出旋转路径,进而得出
π=
π+
,即可得出旋转次数;
(3)①首先求出每翻三次翻一周,顶点O所经过的总路线长,进而得出三角形共翻四周回到初始位置,所以顶点O所经过的总路线长;
②首先求出正方形每翻四次翻一周,顶点O所经过的总路线长,再利用共翻5周回到初始位置,即可得出顶点O所经过的总路线长;
(4)边长相等的两个正多边形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的最小公倍数.
(2)①根据正方形旋转一周的路径,;利用弧长公式以及扇形面积公式求出即可;
②利用正方形纸片OABC经过4次旋转得出旋转路径,进而得出
41+20
| ||
| 2 |
20(2+
| ||
| 2 |
| π |
| 2 |
(3)①首先求出每翻三次翻一周,顶点O所经过的总路线长,进而得出三角形共翻四周回到初始位置,所以顶点O所经过的总路线长;
②首先求出正方形每翻四次翻一周,顶点O所经过的总路线长,再利用共翻5周回到初始位置,即可得出顶点O所经过的总路线长;
(4)边长相等的两个正多边形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的最小公倍数.
解答:解:(1)顶点O所经过的总路线长为:
×2=
π;
(2)①顶点O经过的总路线长为:
×2+
=π+
π=
π,
②由①:每翻转一周顶点O经过的总路线长为:
π,
由
π=
π+
即翻转20周后再翻一次,共翻81次.
(3)①每翻三次翻一周,顶点O所经过的总路线长为:
×2=
π,
共翻四周回到初始位置,所以顶点O所经过的总路线长为:
π×4=
π,
②每翻四次翻一周,顶点O所经过的总路线长为:
×2+
=
+
,
共翻5周回到初始位置,所以顶点O所经过的总路线长为:
5×(
+
)=
π,
(4)当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的最小公倍数.
故答案为:最小公倍数.
| 120π×1 |
| 180 |
| 4 |
| 3 |
(2)①顶点O经过的总路线长为:
| 90π×1 |
| 180 |
90π×
| ||
| 180 |
| ||
| 2 |
2+
| ||
| 2 |
②由①:每翻转一周顶点O经过的总路线长为:
2+
| ||
| 2 |
由
41+20
| ||
| 2 |
20(2+
| ||
| 2 |
| π |
| 2 |
即翻转20周后再翻一次,共翻81次.
(3)①每翻三次翻一周,顶点O所经过的总路线长为:
| 210π×1 |
| 180 |
| 7 |
| 3 |
共翻四周回到初始位置,所以顶点O所经过的总路线长为:
| 7 |
| 3 |
| 28 |
| 3 |
②每翻四次翻一周,顶点O所经过的总路线长为:
| 162π×1 |
| 180 |
162π×
| ||
| 180 |
| 81π |
| 45 |
9
| ||
| 10 |
共翻5周回到初始位置,所以顶点O所经过的总路线长为:
5×(
| 81π |
| 45 |
9
| ||
| 10 |
18+9
| ||
| 2 |
(4)当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的最小公倍数.
故答案为:最小公倍数.
点评:此题主要考查了旋转的性质以及等边三角形的性质和正方形的性质以及弧长公式等知识,熟练利用正多边形的性质以及弧长公式是解题关键.

练习册系列答案
相关题目