题目内容
【阅读】
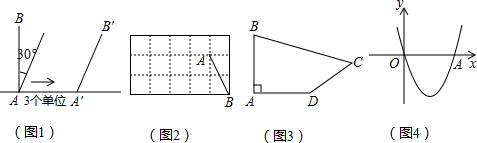
定义:以线段l的一个端点为旋转中心,将这条线段顺时针旋转α(0°<α≤360°),再沿水平向右的方向平移m个单位后得到线段l′(若m<0,则表示沿水平向左的方向平移|m|个单位),称线段l到线段l′的变换为XP<α,m>.图1中的变换XP<30°,3>就表示线段AB绕点A顺时针旋转30°,再沿水平向右的方向平移3个单位后得到线段A′B′的过程.
【操作】
图2是边长为1的正方形网格,线段AB的端点在格点上,以A为旋转中心,在图中画出线段AB经过变换XP<90°,-2>后的对应线段A′B′.
【应用1】
若将与水平方向垂直的线段AB经变换XP<60°,m>后所得的图形是线段CD(如图3),其中点A为旋转中心,AB=4,∠C=45°,求m的值.
【应用2】
如图4,在平面直角坐标系xOy中,其中x轴的正方向为水平向右.若抛物线y=
x2-2x交x轴的正半轴于A,以O为旋转中心,线段OA经过XP<α,m>变换后对应线段的一个端点正好落在抛物线的顶点处,其中请直接写出所有符合题意的α和m的值.
定义:以线段l的一个端点为旋转中心,将这条线段顺时针旋转α(0°<α≤360°),再沿水平向右的方向平移m个单位后得到线段l′(若m<0,则表示沿水平向左的方向平移|m|个单位),称线段l到线段l′的变换为XP<α,m>.图1中的变换XP<30°,3>就表示线段AB绕点A顺时针旋转30°,再沿水平向右的方向平移3个单位后得到线段A′B′的过程.

【操作】
图2是边长为1的正方形网格,线段AB的端点在格点上,以A为旋转中心,在图中画出线段AB经过变换XP<90°,-2>后的对应线段A′B′.
【应用1】
若将与水平方向垂直的线段AB经变换XP<60°,m>后所得的图形是线段CD(如图3),其中点A为旋转中心,AB=4,∠C=45°,求m的值.
【应用2】
如图4,在平面直角坐标系xOy中,其中x轴的正方向为水平向右.若抛物线y=
| 1 |
| 2 |
考点:二次函数综合题
专题:
分析:(1)如图2所示;
(2)【应用1】如图3所示,根据题意可知∠A=90°∠ADC=150°,根据等边三角形的性质,平行四边形的性质求得∠PCB=∠PBC,进而求得PB=PC,得出四边形APCD是菱形,从而求得m的值;
(3)【应用2】,由抛物线y=
x2-2x交x轴的正半轴于A,求得A的坐标顶点坐标,进而求得OA=4,分两种情况分别讨论求得;
(2)【应用1】如图3所示,根据题意可知∠A=90°∠ADC=150°,根据等边三角形的性质,平行四边形的性质求得∠PCB=∠PBC,进而求得PB=PC,得出四边形APCD是菱形,从而求得m的值;
(3)【应用2】,由抛物线y=
| 1 |
| 2 |
解答: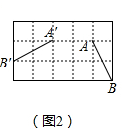
解:(1)【操作】,如图2;
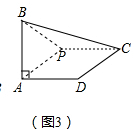
(2)【应用1】如图3所示,根据题意可知∠A=90°∠ADC=150°,
∵∠C=45°,
∴∠B=75°,
∵AB=AP=4,∠BAP=60°,
∴三角形APB是等边三角形,
AP=PB=AB=4,∠APB=60°,
∴∠PBC=15°,∠PAD=30°,
∵AP=DC,AP∥DC,
∴四边形APCD是平行四边形,
∴AP=CD=4,∠PCD=∠PAD=30°,
∴∠PCB=15°,
∴∠PCB=∠PBC,
∴PB=PC,
∴四边形APCD是菱形,
∴AD=AP=AB=4,
即m=4;
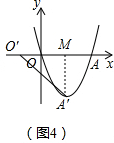
(3)【应用2】有两种情况:
如图4所示,∵抛物线y=
x2-2x交x轴的正半轴于A,
∴令y=0,y=
x2-2x=0,
解得:x=0,x=4,
∴A(0,4),
∴OA=4,
由抛物线y=
x2-2x可知顶点坐标A′为(2,2),
∴AM=2
∵O′A′=OA=4,
则sin∠A′O′M=
=
,
∴∠A′O′M=30°,
即α=30°;
∴O′M=2
,
∴OO′=2
-2,
即m=2-2
;

如图4所示:∠A″OA=150°,O′M=2
,
所以,α=150°和m=2+2
.

解:(1)【操作】,如图2;

(2)【应用1】如图3所示,根据题意可知∠A=90°∠ADC=150°,
∵∠C=45°,
∴∠B=75°,
∵AB=AP=4,∠BAP=60°,
∴三角形APB是等边三角形,
AP=PB=AB=4,∠APB=60°,
∴∠PBC=15°,∠PAD=30°,
∵AP=DC,AP∥DC,
∴四边形APCD是平行四边形,
∴AP=CD=4,∠PCD=∠PAD=30°,
∴∠PCB=15°,
∴∠PCB=∠PBC,
∴PB=PC,
∴四边形APCD是菱形,
∴AD=AP=AB=4,
即m=4;

(3)【应用2】有两种情况:
如图4所示,∵抛物线y=
| 1 |
| 2 |
∴令y=0,y=
| 1 |
| 2 |
解得:x=0,x=4,
∴A(0,4),
∴OA=4,
由抛物线y=
| 1 |
| 2 |
∴AM=2
∵O′A′=OA=4,
则sin∠A′O′M=
| A′M |
| O′A′ |
| 1 |
| 2 |
∴∠A′O′M=30°,
即α=30°;
∴O′M=2
| 3 |
∴OO′=2
| 3 |
即m=2-2
| 3 |

如图4所示:∠A″OA=150°,O′M=2
| 3 |
所以,α=150°和m=2+2
| 3 |
点评:本题考查旋转的性质,平移的性质,等边三角形的判定和性质,菱形的判定和性质,抛物线的交点和顶点的坐标的求法,解直角三角函数等;

练习册系列答案
相关题目
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=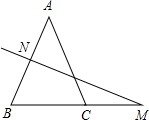 已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.