Question

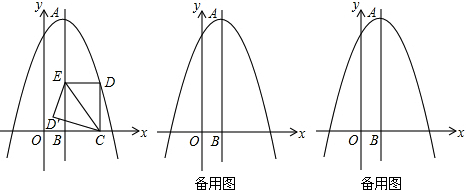
如图，已知平行四边形ABCD的BC边在x轴上，A、D两点分别在反比例函数y=-

2

x

和y=

k

x

图象上，若S_?ABCD=8，则k=

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：

分析：由已知可得点A和点D的纵坐标相等，设出点A，D的坐标用y与k的式子表示出AD，利用平行四边形的面积可求出k的值．

解答：解：∵平行四边形ABCD的BC边在x轴上，A、D两点分别在反比例函数y=-

2

x

和y=

k

x

图象上，
∴设A点的坐标为（x₁，y），点D的坐标为（x₂，y），
∴AD=x₂-x₁=

k

y

-（-

2

y

）=

k+2

y

，
∵S_?ABCD=8，
∴AD•y=8，
∴

k+2

y

•y=8，
∴k+2=8，
解得k=6，
故答案为：6．

点评：本题主要考查了反比例函数系数k的几何意义，解题的关键是用y与k的式子表示出AD．