题目内容
13. 如图,△ABC中,AC=BC,D、E分别是AB、AC的中点,若AC=6,AB=4,则△ADE的周长是8.
如图,△ABC中,AC=BC,D、E分别是AB、AC的中点,若AC=6,AB=4,则△ADE的周长是8.
分析 首先根据三角形中位线的性质可得DE=$\frac{1}{2}$BC=3,再根据中点定义可得AD=2,AE=3,然后求周长即可.
解答 解:∵AC=BC,
∴BC=6,
∵D、E分别是AB、AC的中点,
∴DE=$\frac{1}{2}$BC=3,AD=2,AE=3,
∴△ADE的周长是:2+3+3=8.
故答案为:8.
点评 此题主要考查了三角形的中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列从左到右的变形中,属于因式分解的是( )
| A. | (x+y)(x-2y)=x2-xy+y2 | B. | 3x2-x=x(3x-1) | ||
| C. | (a-b)2=(a-b)(a-b) | D. | m2-n2=(m-n)2 |
8.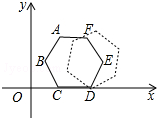 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(50,2)的是( )| A. | 点A | B. | 点B | C. | 点 C | D. | 点D |
3. 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )| A. | 65° | B. | 25° | C. | 30° | D. | 15° |