题目内容
2.已知(2x-1)8=a8x8+a7x7+a6x6+…+a1x+a0(1)a8的值;
(2)a0的值;
(3)a8+a6+a4+a2的值.
分析 (1)${a}_{8}{x}^{8}=(2x)^{8}$;
(2)${a}_{0}=(-1)^{8}$;
(3)令x=1,x=-1,分别求得代数式的值,然后将两式相加再除2即可.
解答 解:(1)∵${a}_{8}{x}^{8}=(2x)^{8}$,
∴${a}_{8}={2}^{8}=256$.
(2)∵a0不含x,
∴${a}_{0}=(-1)^{8}$.
∴a0=1.
(3)令x=1得;a8+a7+a6+a5+a4+a3+a2+a1+a0=1.
令x=-1得;a8-a7+a6-a5+a4-a3+a2-a1+a0=6561
∴2(a8+a6+a4+a2)=6562.
∴a8+a6+a4+a2=3281.
点评 本题主要考查的是二项式定理的应用,掌握二项展开式通项公式是解题的关键.

练习册系列答案
相关题目
10.下列长度的三条线段能组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 3cm,4cm,8cm | C. | 5cm,12cm,13cm | D. | 5cm,8cm,15cm |
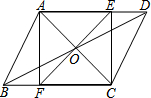 在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证:
在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求证: 如图,△ABC中,AC=BC,D、E分别是AB、AC的中点,若AC=6,AB=4,则△ADE的周长是8.
如图,△ABC中,AC=BC,D、E分别是AB、AC的中点,若AC=6,AB=4,则△ADE的周长是8.