��Ŀ����
18����ͼ��ֱ��y=kx+k��x�ᣬy��ֱ���A��C��ֱ��BC����C��x����B��OC=3OA����CBA=45�㣮��1����ֱ��BC�Ľ���ʽ��
��2������P��A����������AB�����˶����ٶ�Ϊ2����λ/�룬����CP�����PBC�����ΪS����P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��ֱ��д��t��ȡֵ��Χ��
��3���ڣ�2���������£�����P��AB���ӳ������˶�ʱ������O��OD��PC��D����BC�ڵ�E������AE������EAB=��CPAʱ�������������е�K����KC=KP�����K�����꣮
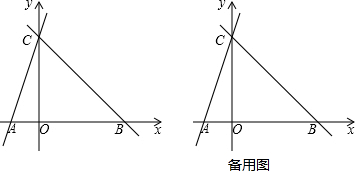
���� ��1����y=0���������A�����꣬����OC=3OA�������C�����꣬�ٸ��ݡ�CBA=45�㣬����BOC�ĵ���ֱ�������Σ���B�����꼴����ã�Ȼ�����ô���ϵ�������BC�Ľ���ʽ��
��2���ֳ�P��AB����AB���ӳ�������������������ۣ����������������ʽ������⣻
��3����P�������ǣ�2t-1��0�������ô���ϵ�������PC�Ľ���ʽ��O��OD��PC��D������AD������DAB=��CPA����D�ĺ�������AB���е�ĺ�������ȣ���D��AB�ľ������$\frac{1}{2}$AB����D�����꼴������t��ʾ������Ȼ�����PC�Ľ���ʽ���t��ֵ�����ɵõ�P�����꣬������⣮
��� �⣺��1����y=kx+k�У���y=0����x=-1����A�������ǣ�-1��0����
��OC=3OA��
��OC=3����C�������ǣ�0��3����
�ߡ�CBA=45�㣬
���OCB=��CBA=45�㣬
��OB=OC=3����B�������ǣ�3��0����
��BC�Ľ���ʽ��y=kx+b����$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��BC�Ľ���ʽ��y=-x+3��
��2����0��t��2ʱ��P���߶�AB�ϣ���BP=4-2t��
��S=$\frac{1}{2}$��4-2t����3=-3t+6��
��t��2ʱ��OP=2t-4����S=$\frac{1}{2}$��3��2t-4������S=3t-6��
��3����DF��AB�ڵ�F��
��P�������ǣ�2t-1��0����A�������ǣ�-1��0����
��D�������$\frac{2t-1-1}{2}$=t-1��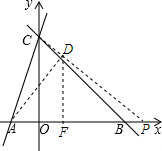
��AD��CP����DAB=��CPA����AD=DP��
���ADB�ǵ���ֱ�������Σ�
�֡�DF��AB�ڵ�F��
��DF=$\frac{1}{2}$AP=t����D�������ǣ�t-1��t����
��PC�Ľ���ʽ��y=mx+n����$\left\{\begin{array}{l}{n=3}\\{��2t-1��m+n=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=\frac{3}{1-2t}}\\{n=3}\end{array}\right.$��
��PC�Ľ���ʽ��y=$\frac{3}{1-2t}$x+3��
��D�������ǣ�t-1��t�����������ʽ�ã�$\frac{3}{1-2t}$•��t-1��=t��
��ã�t=2��0����ȥ����
��P�������ǣ�3��0����
��PC�Ľ���ʽ��y=-x+3��
��B��P�غϣ���OC=OB��KC=KP��
��K��O�غϣ���K�������ǣ�0��0����
���� ���⿼���˴���ϵ���������Ľ���ʽ���Լ�����ֱ�������ε��ж������ʣ�����Ĺؼ���ѧ�����ò���������⣬��ȷ���D�������DZ����ͻ�Ƶ㣮

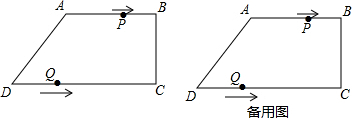
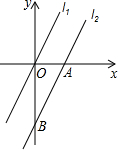 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��Ӧ�ĺ�������ʽΪy=2x��ֱ��l2��x�ᡢy��ֱ��ڵ�A��B����l1��l2��OA=2�����߶�OB�ij�Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��Ӧ�ĺ�������ʽΪy=2x��ֱ��l2��x�ᡢy��ֱ��ڵ�A��B����l1��l2��OA=2�����߶�OB�ij�Ϊ��������| A�� | 3 | B�� | 4 | C�� | 2$\sqrt{2}$ | D�� | 2 |
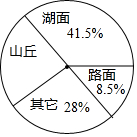 ��������ȥij��ռ�طֲ����ͳ��ͼ��
��������ȥij��ռ�طֲ����ͳ��ͼ����1������ռ��������·��ռ�������С��
��2��ɽ��ռ����22%��
��3�����蹫ռ��1200���꣬����д�±���
| ռ������ | ���� | ɽ�� | ·�� | ���� |
| ռ����������꣩ | 498 | 264 | 102 | 336 |
| A�� | AB��CD��AD��BC | B�� | AB=AD��CB=CD | C�� | AB=CD��AC=BD | D�� | ��A=��B����C=��D |
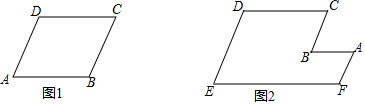
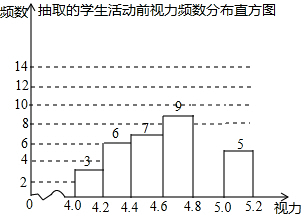 Ϊ�˱���������ѧУ�ƻ���չ�����ۻ��ۡ������������Ϊʹ�������ʵЧ�ԣ��ȶ�ѧ������������е��飬�����ȡ40��ѧ����������ǵ������������Ʋ�������ֱ��ͼ�����ݰ�����˵㲻�����Ҷ˵㣬��ȷ��0.1��������ֱ��ͼ����Ϣ����������⣺
Ϊ�˱���������ѧУ�ƻ���չ�����ۻ��ۡ������������Ϊʹ�������ʵЧ�ԣ��ȶ�ѧ������������е��飬�����ȡ40��ѧ����������ǵ������������Ʋ�������ֱ��ͼ�����ݰ�����˵㲻�����Ҷ˵㣬��ȷ��0.1��������ֱ��ͼ����Ϣ����������⣺