题目内容
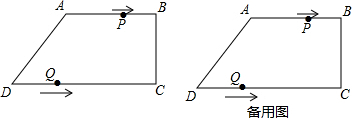
10.如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,但个点P到达B点火点Q到达C点时,P、Q运动停止,设运动时间为t.(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理由.
分析 (1)作AM⊥CD于M,则由题意四边形ABCM是矩形,在Rt△ADM中,利用勾股定理求出DM,根据CD=DM+CM=DM+AB计算即可;
(2)当BP=DQ时,四边形PBQD是平行四边形,可得10-2t=3t,推出t=2,此时BP=DQ=6,CQ=10,因为BQ=$\sqrt{B{C}^{2}+C{Q}^{2}}$=$\sqrt{{8}^{2}+1{0}^{2}}$=2$\sqrt{41}$,所以根据四边形PBQD的周长=2(BP+BQ)计算即可;
(3)不存在.不妨设存在,列出方程求出时间t,再说明t不符合题意即可;
解答 解:(1)作AM⊥CD于M,则由题意四边形ABCM是矩形,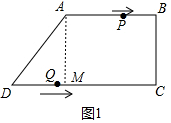
在Rt△ADM中,∵DM2=AD2-AM2,AD=10,AM=BC=8,
∴AM=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴CD=DM+CM=DM+AB=6+10=16.
(2)当四边形PBQD是平行四边形时,点P在AB上,点Q在DC上,如图2中,由题意:BP=AB-AP=10-2t.DQ=3t,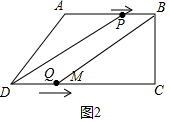
当BP=DQ时,四边形PBQD是平行四边形,
∴10-2t=3t,
∴t=2,此时BP=DQ=6,CQ=10,
∴BQ=$\sqrt{B{C}^{2}+C{Q}^{2}}$=$\sqrt{{8}^{2}+1{0}^{2}}$=2$\sqrt{41}$,
∴四边形PBQD的周长=2(BP+BQ)=2(6+2$\sqrt{41}$)=12+4$\sqrt{41}$.
(3)不存在.理由如下:
作AM⊥CD于M,连接PQ.由题意AP=2t.DQ=3t,
由(1)可知DM=6,
∴MQ=3t-6,
若2t=3t-6,
解得t=6,
∵AB=10,
∴t≤$\frac{10}{2}$=5,
而t=6>5,故t=6不符合题意,t不存在.
点评 本题考查四边形综合题、平行四边形的判定和性质、矩形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考常考题型.

| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法判断 |
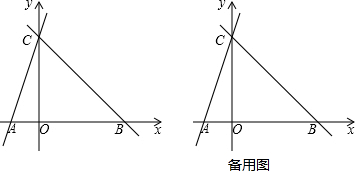
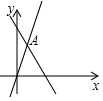 如图,已知函数y=3x和y=ax+5的图象相交于点A(n,3),则不等式3x>ax+5的解集为( )
如图,已知函数y=3x和y=ax+5的图象相交于点A(n,3),则不等式3x>ax+5的解集为( )| A. | x<0 | B. | x<1 | C. | x>1 | D. | x>3 |
 如图,在?ABCD中,CH⊥AD于点H,CH与BD的交点为E,如果∠1=70°,∠ABC=3∠2,那么∠ADC=60°.
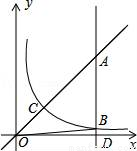
如图,在?ABCD中,CH⊥AD于点H,CH与BD的交点为E,如果∠1=70°,∠ABC=3∠2,那么∠ADC=60°.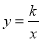 (x>0)上一点,直线AB平行于y轴交直线y=x于点A,交x轴于点D,
(x>0)上一点,直线AB平行于y轴交直线y=x于点A,交x轴于点D, 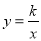 与直线y=x交于点C,若OB2﹣AB2=4
与直线y=x交于点C,若OB2﹣AB2=4